Python实现平衡二叉树的代码与原理

平衡二叉树是一种特殊的二叉搜索树，它的主要特点是任何节点的左子树和右子树的高度差的绝对值不超过1，确保了树的结构尽可能均衡。在Python中实现平衡二叉树的关键在于维护每个节点的左右子树高度，并在插入或删除节点时进行相应的调整。 首先，我们需要定义一个节点类`Node`，它包含四个属性：左子节点（`left_children`）、左子树高度（`left_height`）、右子节点（`right_children`）和右子树高度（`right_height`），以及节点的值（`value`）。这个类初始化时，这些属性默认为None。 接着，我们定义二叉树类`BinarySearchTree`，它包含根节点（`root`）和三个列表：`front_list`用于存储未插入的节点，`middle_list`用于存储正在处理的节点，`after_list`用于存储已经插入的节点。这个类有两个方法：`__init__`用于初始化空树，以及`create_tree`用于根据输入的有序列表生成平衡二叉树。 在`create_tree`方法中，首先检查输入列表是否为空，然后递归地处理列表中的每个元素。对于每个元素，创建一个新的节点，将其值设置为该元素，然后根据以下策略调整树的结构： 1. 如果当前节点是根节点（`not self.root`），则设置当前节点为根并清空列表。 2. 检查列表是否已为空，如果为空则打印错误信息并返回。 3. 当待插入的索引`n`超出列表范围时，说明已达到末尾，提示生成完成并返回。 4. 创建新节点，将列表的第`n`个元素赋值给节点的值。 5. 根据当前节点的状态，将其添加到相应列表中，以便后续处理：`front_list`表示未处理的节点，`middle_list`表示当前正在处理的节点，`after_list`表示已经处理过的节点。 当列表中所有元素都被处理后，`front_list`应为空，`middle_list`中的节点都已经按照平衡二叉树规则进行了调整。通过这样的方式，我们可以在插入操作时保持树的平衡性，避免出现高度差过大导致的性能问题。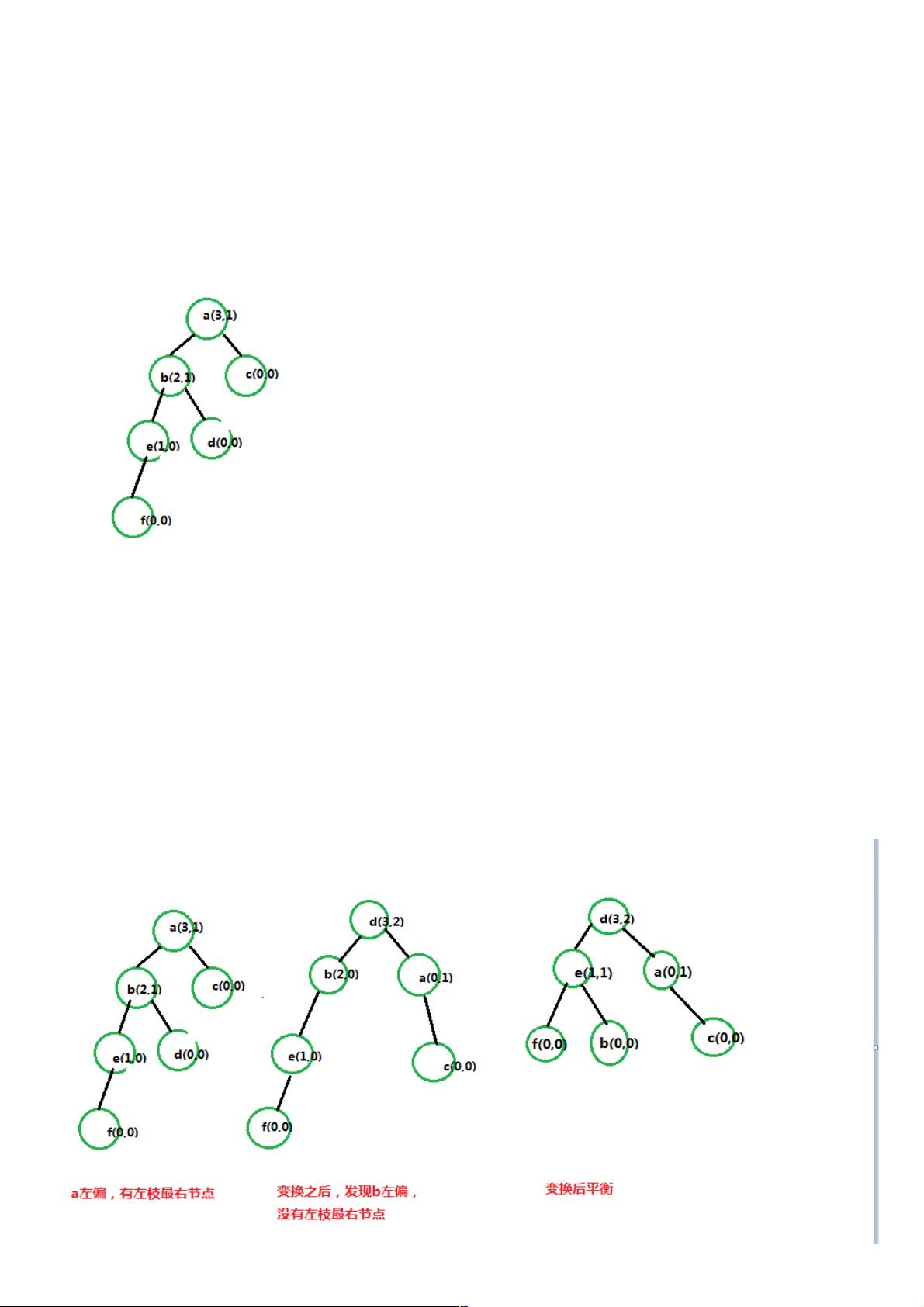 平衡二叉树的构建过程依赖于对节点进行旋转操作，包括左旋和右旋，来维持平衡。当发现某节点高度差超过1时，根据具体情况选择旋转操作。例如，如果左子树高度大于右子树高度，可能需要进行右旋；反之，如果右子树高度大于左子树高度，则需要进行左旋。这些旋转操作的具体实现会在实际代码中体现，但在这段描述中并未给出详细的代码示例。 总结起来，这段代码提供了一个基础的框架，用于实现平衡二叉树的节点类和树类，以及如何根据输入列表生成平衡二叉树。关键在于理解平衡二叉树的定义和调整规则，并在实际操作中应用这些规则来维护树的平衡。