多视图维共约化：无监督降维新方法
164 浏览量
更新于2024-08-26
收藏 3.41MB PDF 举报
"灵活的多视图维共约化"是一篇发表在2017年2月IEEE Transactions on Image Processing的论文，针对具有多个视图的高维数据进行无监督降维研究。在信息技术领域，维度降低（dimensionality reduction）是一项关键任务，其目标是将高维输入映射到低维子空间，使得相似的数据点彼此靠近，反之亦然。本文的主要贡献在于提出了一种创新方法——多视图维共约化（Multi-view Dimensionality Co-Reduction），它专注于有效利用多视图数据之间的互补性。
该方法的核心理念是灵活地处理不同视图之间的关系，确保在降维过程中保持数据点间相似性的连贯性。论文作者利用希尔伯特-施密特独立性准则（Hilbert-Schmidt Independence Criterion）下的核匹配约束，强化了不同视图之间的关联，并对它们之间的分歧进行惩罚。具体来说，该方法独立地探索每个视图内的相关性，并通过核匹配的方式联合最大化不同视图间的依赖性。这样做的目的是在保持局部结构的同时，实现跨视图数据的有效整合。
在实现上，该方法可能包括以下步骤：
1. 数据预处理：对每个视图进行独立的特征提取和表示学习。
2. 单视图降维：利用核方法（如核主成分分析或核独立成分分析）在每个视图内找到低维嵌入。
3. 核匹配：通过希尔伯特-施密特内积计算不同视图的潜在空间中的相似性，并应用核匹配算法来优化整个数据集的嵌入一致性。
4. 合并低维表示：将单视图的降维结果结合在一起，形成一个共享的低维空间，其中数据点的相似性得到增强。
这种方法的优势在于能够在无标签的情况下，挖掘出数据的内在结构和潜在规律，这对于许多机器学习任务，如图像识别、视频分析和多模态数据融合至关重要。通过这种灵活的多视图降维策略，可以显著提高模型的性能和鲁棒性，为后续的数据分析和决策提供更加简洁且富有洞察力的表示。
650 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 26, NO. 2, FEBRUARY 2017
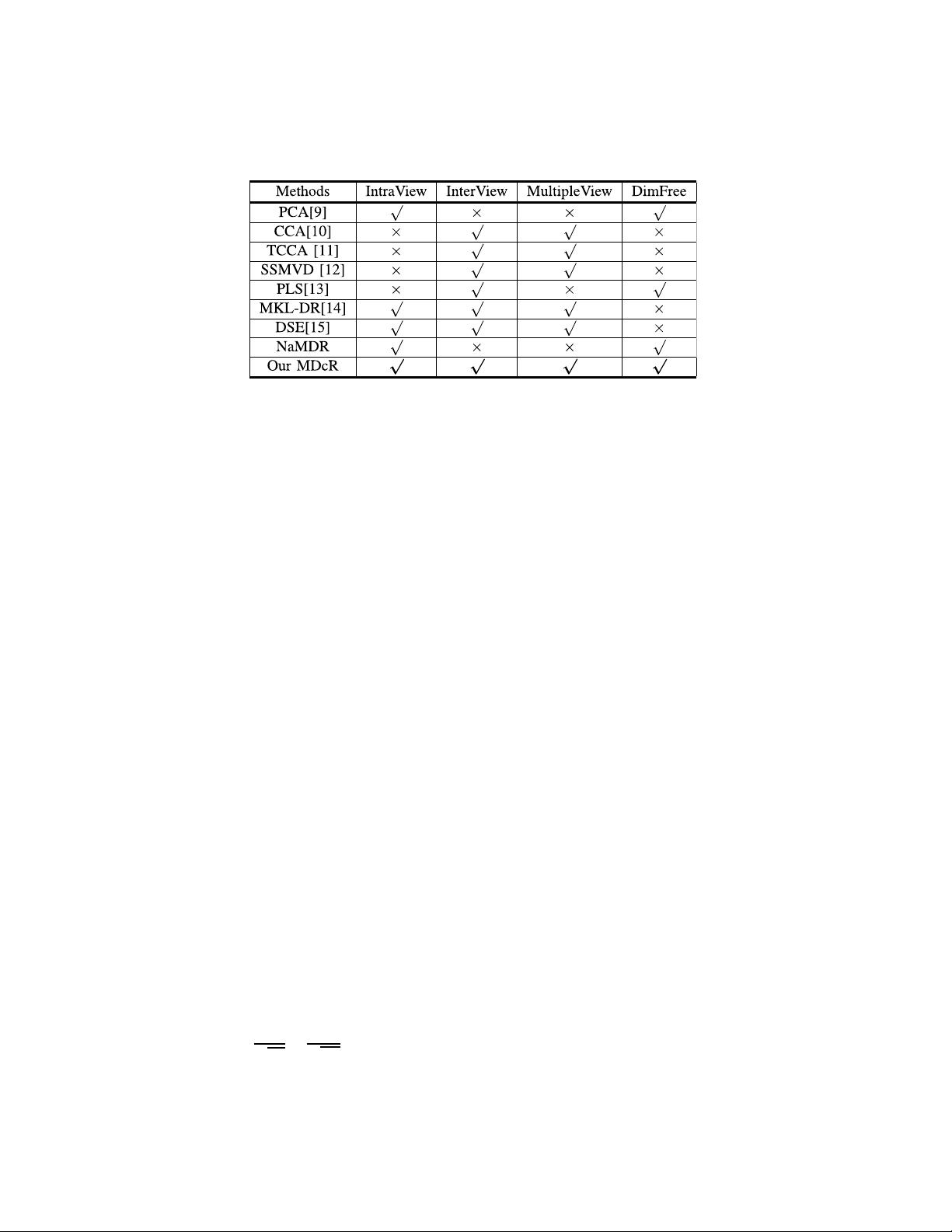
TABLE I
C
OMPARISON OF UNSUPERVISED MULTI-VIEW DIMENSIONALITY REDUCTION METHODS.INTRAVIEW:EXPLORING THE CORRELATIONS WITHIN
EACH VIEW,INTERVIEW:EXPLORING THE CORRELATIONS ACROSS THE DIFFERENT VIEWS,MULTIPLEVIEW:APPLIED FOR THE
DATA WITH MORE THAN 2VIEWS,DIMFREE:FREE OF REDUCING EACH VIEW TO A COMMON SPACE (‘
√
’ AND ‘×’INDICATE
PRESENCE AND ABSENCE OF PROPERTY,RESPECTIVELY)
is measured by HSIC. It employs the inner product kernel
as well as two nonlinear kernels. However, the optimization
for nonlinear case is not such efficient. In the work [35],
the authors exploit the criterion HSIC in a semi-supervised
manner to map pairs of instances to each other without exact
correspondence requirement. The work [32] performs self-
based subspace clustering with multiple views, while the HSIC
is used for diversity measure. In our work, we make our goal
to perform multi-view dimensionality reduction jointly. To this
end, we learn the low-dimensional projection for each view
by maximizing HSIC over the kernel matrices to explore the
correlations across these multiple views.
III. T
HE PROPOSED METHOD
We firstly give a brief introduction for graph embedding
dimensionality reduction [39]. Then we will detail the HSIC
for kernel matching and induce the proposed MDcR method.
A. Graph Embedding Dimensionality Reduction
Graph embedding dimensionality reduction [39] aims to
perform dimensionality reduction with local relationships of
points preserved. Given X =[x
1
, x
2
,...,x
N
]∈R
D×N
with
each column being a sample vector, the goal of dimensional-
ity reduction is obtaining the corresponding low-dimensional
representation Z =[z
1
, z
2
,...,z
N
]∈R
K ×N
,whereK D
and z
i
is the low-dimensional representation of x
i
.Forthe
graph embedding based dimensionality reduction method [39],
the objective is designed to ensure the sufficiently smooth on
the the data manifold. The intuitive explanation is that if two
data points x
i
and x
j
are close, then their low-dimensional
representations z
i
and z
j
should be similar to each other. The
distance of two low-dimensional representations z
i
and z
j
is
defined as
d(z
i
, z
j
) =||
z
i
√
d
ii
−
z
j
d
jj
||
2
, (1)
where the distance is normalized by d
ii
and d
jj
in order to
reduce the impact of popularity of nodes as in traditional
graph-based learning [40], [41], and D is a diagonal matrix
with element d
ii
=
n
j=1
w
ij
. W = (w
ij
) is the affinity
matrix, which is often constructed by the original data
matrix X. Then, the graph-regularized representation can be
learned by the following objective function
min
Z∈R
K×N
ij
||z
i
− z
j
||
2
w
ij
= max
Z∈R
K×N
tr(ZLZ
T
), (2)
where L = D
−1/2
WD
−1/2
is the normalized graph Laplacian
matrix, and tr(·) denotes the trace of a matrix.
For the multi-view setting, a naive way is incorporating
multiple views directly as
max
Z
(v)
∈R
K
(v)
×N
V
v=1
tr(Z
(v)
L
(v)
Z
(v)
T
), (3)
where v denotes the view index. Z
(v)
and L
(v)
denote the
learned low-dimensional representation and the normalized
graph Laplacian matrix corresponding to the v
th
view, respec-
tively. For explicitly learning the projections between high-
dimensional and low-dimensional spaces, the projection P
(v)
is introduced as Z
(v)
= P
(v)
X
(v)
for the v
th
view. Accordingly,
the objective function in Eq. (3) is derived as
max
P
(v)
∈R
K
(v)
×D
(v)
V
v=1
tr(P
(v)
X
(v)
L
(v)
X
(v)
T
P
(v)
T
)
s.t. P
(v)
P
(v)
T
= I,v = 1,...,V, (4)
where D
(v)
and K
(v)
correspond to the dimensionalities of
the original (high-dimensional) space and the corresponding
reduced (low-dimensional) subspace, respectively. The con-
straint P
(v)
P
(v)
T
= I prevents the trivial solution. Intuitively,
this naive way reduces the dimensionality of each view
independently and does not exploit the correlations of these
multiple views.
B. Kernel Matching via HSIC
In this work, we introduce Hilbert Schmidt Independence
Criterion (HSIC) [36] to explore the correlations among
different views, which has the following advantages [38].
First, HSIC measures dependence of the reduced subspaces of
different views by mapping variables into a reproducing kernel
Hilbert space (RKHS) such that these views need not depend
on a common low-dimensional subspace, which is critical to
剩余11页未读，继续阅读
2010-08-28 上传
点击了解资源详情
点击了解资源详情
2024-11-09 上传
2024-11-09 上传
weixin_38546024
- 粉丝: 6
- 资源: 939
我的内容管理
展开
最新资源
- Fisher Iris Setosa数据的主成分分析及可视化- Matlab实现
- 深入理解JavaScript类与面向对象编程
- Argspect-0.0.1版本Python包发布与使用说明
- OpenNetAdmin v09.07.15 PHP项目源码下载
- 掌握Node.js: 构建高性能Web服务器与应用程序
- Matlab矢量绘图工具：polarG函数使用详解
- 实现Vue.js中PDF文件的签名显示功能
- 开源项目PSPSolver：资源约束调度问题求解器库
- 探索vwru系统：大众的虚拟现实招聘平台
- 深入理解cJSON：案例与源文件解析
- 多边形扩展算法在MATLAB中的应用与实现
- 用React类组件创建迷你待办事项列表指南
- Python库setuptools-58.5.3助力高效开发
- fmfiles工具：在MATLAB中查找丢失文件并列出错误
- 老枪二级域名系统PHP源码简易版发布
- 探索DOSGUI开源库：C/C++图形界面开发新篇章
