分数阶电路解析解与数值模拟：Laplace变换与非标准差分解法

本文主要探讨了分数阶线性电系统在工程领域的应用及其解析解与数值模拟分析。分数阶微积分作为一种新兴的数学工具，因其能够有效描述具有记忆效应和非局部性质的材料和过程，如含有超级电容和超级电感的电路，近年来受到了广泛关注。作者们，W.K. Zahra、M.M.塔希尔·希卡尔巴赫纳西和T.A. Bahnasy，基于埃及坦塔大学和日本科学技术大学的研究背景，对分数阶电路的建模采用了一种创新的方法。 首先，他们利用拉普拉斯变换这一经典数学工具，对分数阶电路模型进行了分析，成功导出了分数阶系统的解析解。拉普拉斯变换在此起到了关键作用，它将微分方程转化为代数方程，使得复杂的时间域问题在复频域中变得更容易处理。这种方法在处理线性电路问题时展现了其优势，尤其是在与经典电系统进行对比时，能够清晰地展现分数阶系统特有的特性。 此外，作者们还引入了Grünwald-Letnikov定义的数值模拟技术，这是一种针对分数阶导数的数值方法，它在解决实际问题时提供了可靠的数值近似。通过这种数值模拟，他们不仅验证了分数阶电路模型的解析解，而且能够处理那些难以解析求解的非标准情况。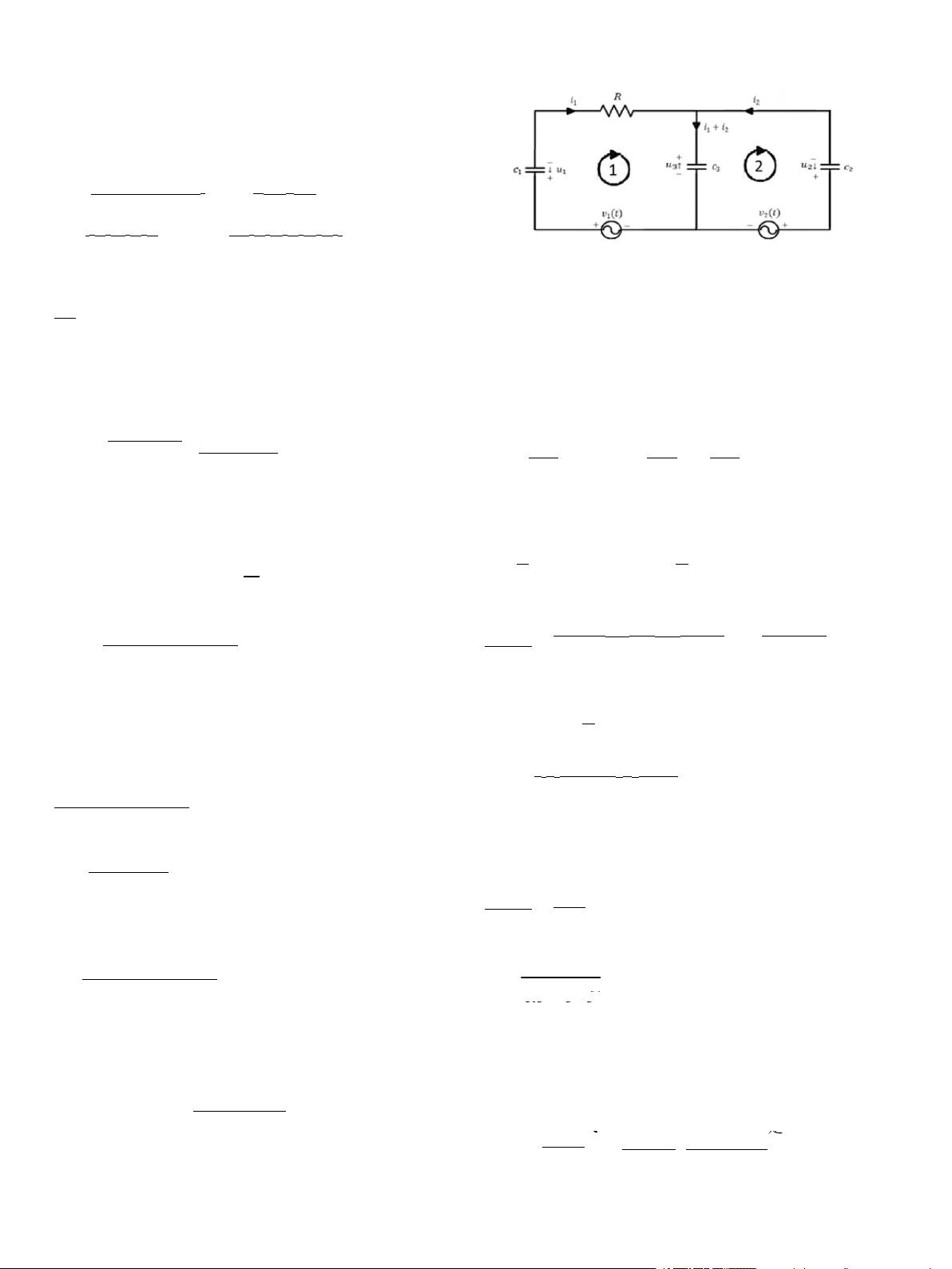 在文中，他们以RLC电路为例，展示了分数阶微积分如何应用于电路分析，包括电路的充电和放电过程，以及非局部行为的研究。通过Adomian分解法和拉普拉斯变换的结合，他们探讨了电路解的存在唯一性，这在电路设计和控制中具有重要意义。 最后，作者们强调了分数阶系统在电路工程中的潜在应用价值，并指出他们的研究成果是开放获取的，受到Creative Commons Attribution-NonCommercial-NoDerivatives (CC BY-NC-ND) 许可。这项工作不仅提升了我们对分数阶电路的理解，也为后续的理论研究和工程实践提供了宝贵的基础。 本文是一篇深入研究分数阶线性电系统分析的重要文献，通过理论分析和数值模拟，为电路设计者提供了处理非整数阶电路的新视角和技术手段。它在推动分数阶微积分在工程领域的发展，尤其是在分数阶电路设计和故障诊断中的应用方面，具有重要的贡献。