"深入理解正态分布：常用概率分布PPT详解"

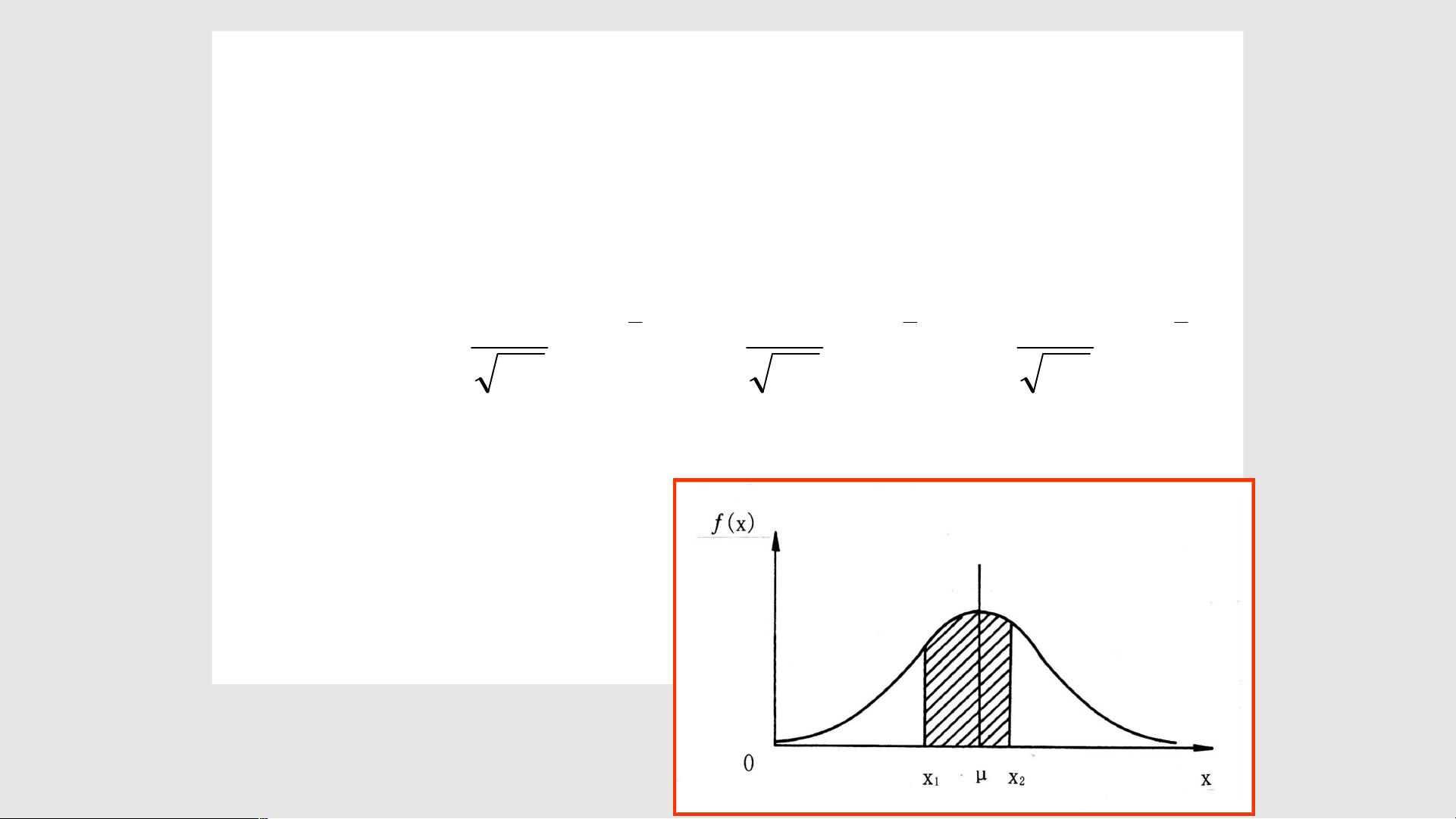
正态分布是一种常见的概率分布，其具有单峰、对称的钟形曲线特征。正态分布的定义是，若连续型随机变量 x 的概率分布密度函数为 f(x) = (1/(σ√(2π))) * exp(-(x-μ)²/(2σ²))，其中 μ 为平均数， σ² 为方差，则称随机变量 x 服从正态分布，记为 x ～ N(μ,σ²) 。正态分布的概率密度函数曲线在 x=μ 处对称，达到极大值，且是非负函数，以 x 轴为渐近线，分布从负无穷到正无穷。在 x=μ±σ 处各有一个拐点，即曲线在 (-∞,μ-σ) 和(μ σ, ∞) 区间上是下凸的，在 [μ-σ,μ σ] 区间内是上凸的。正态分布具有两个参数，即平均数 μ 和标准差 σ。正态分布的密度曲线与横轴所夹的面积为1，这代表着全部可能性的总和为1。 正态分布在统计学领域中有着广泛的应用，尤其是在假设检验、参数估计和回归分析等方面。在实际生活中，许多自然现象也可以用正态分布来描述，例如身高、体重、考试成绩等。正态分布还有一个重要的性质，即当随机变量 x 的分布接近正态分布时，根据中心极限定理，样本均值的分布也会趋于正态分布。这使得正态分布成为很多统计推断方法的基础。 正态分布的应用不仅限于统计学领域，还广泛应用于工程、物理、生物学等领域。例如，在工程领域，正态分布被用于描述机械零件的尺寸精度、电路元件的性能分布等；在物理学中，正态分布可用于描述粒子的速度分布、能级的分布等；在生物学中，正态分布可以描述人口的身高分布、动物的体重分布等。因此，对于研究人员和工程师来说，了解和掌握正态分布是非常重要的。 总的来说，正态分布是自然界和人类社会中普遍存在的一种规律性分布，具有重要的理论和实际意义。通过研究和了解正态分布，可以更好地理解和解释各种现象，提高数据分析和预测的准确性，为科学研究和实践应用提供有力支持。希望通过本课件对正态分布的介绍和解释，能够帮助大家更深入地理解和应用正态分布，为相关领域的研究和实践提供更多价值和启示。