计数器级联规律与应用实例
需积分: 17 36 浏览量
更新于2024-08-12
收藏 194KB PDF 举报
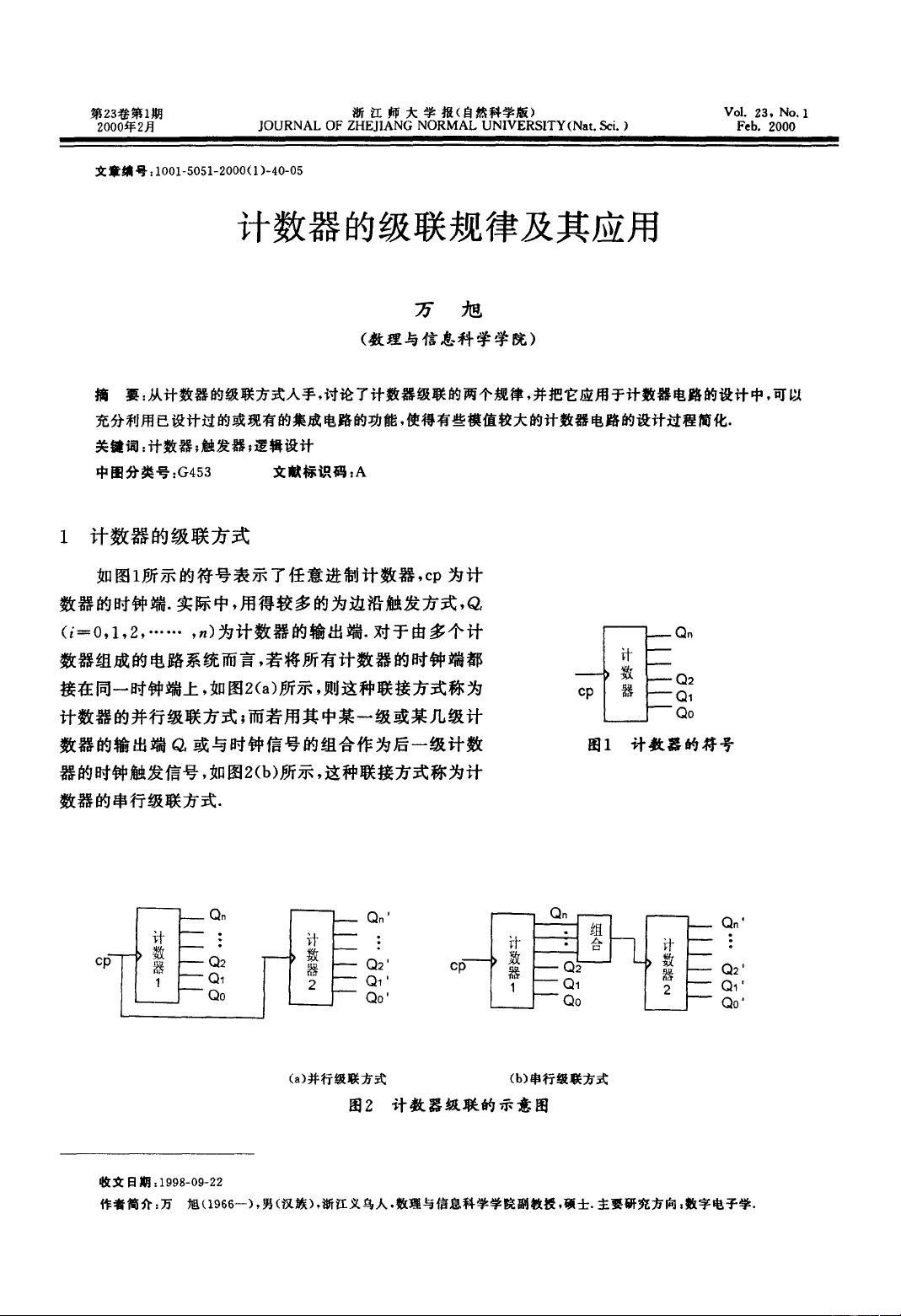
本文主要探讨了计数器的级联规律及其在电路设计中的应用。首先,作者从基本概念出发,解释了计数器的两种主要级联方式:并行级联和串行级联。并行级联是指所有计数器的时钟端共享一个统一的时钟输入,而串行级联则是通过级联的计数器输出作为后续计数器的时钟触发信号。
在并行级联中,作者引入了“可分解计数器”和“因子计数器”的概念。如果一个模为N的计数器可以通过多个较小模值(N1、N2等)的计数器级联得到,那么这个N计数器就是可分解的,而那些较小的计数器则被称为它的因子计数器。本文重点集中在并行级联上,提出了一个关键定理:
定理1指出,当两个计数器,模值分别为N1和N2进行并行级联时,新产生的计数器模值将是这两个模的最小公倍数(LCM)。这个定理为设计者提供了设计复杂计数器电路的一个有效工具,因为它允许利用已知的、具有较小模值的计数器组合来构建所需的较大模值计数器,从而简化设计过程。
作者通过对并行级联方式的深入分析,强调了这种级联方法在节省硬件资源和提高设计效率方面的价值。在实际电路设计中,这不仅能减少设计工作量,还有助于节约成本,特别是当需要较大模值但市场上缺乏相应单一芯片时。
此外,文中还提到了作者的个人信息,万旭教授,他是一名专注于数字电子学领域的副教授,其研究方向为计数器和触发器的逻辑设计。这篇论文不仅提供了理论知识,而且具有很强的实用性,对于从事电子设计和计数器电路研究的专业人士具有很高的参考价值。
这篇文章深入剖析了计数器级联的基本原理,特别是在并行级联中的规律,并将其应用于实际电路设计中,对于提升计数器电路设计的效率和灵活性具有重要意义。
652 浏览量
3471 浏览量
1531 浏览量
138 浏览量
231 浏览量
135 浏览量
183 浏览量
346 浏览量
2023-06-01 上传
weixin_38685857
- 粉丝: 5
- 资源: 890
最新资源
- 第33课
- 行业分类-设备装置-一种扩散性纸张增湿设备.zip
- 电子发票管理系统 衡德电子发票台账 v2.4
- qle:QMK徽标编辑器
- sEMG_Basic_Hand_movements:sEMG 基本手部运动的 Matlab 代码-matlab开发
- 立体像对的空间前方交会-点投影系数法+共线方程严密法(C# winform)
- 塔夫
- ImDisk Toolkit:Windows 版 Ramdisk 和映像文件的挂载-开源
- weatherForcast
- 行业分类-设备装置-一种承托、贴靠式安装的装配式墙体.zip
- 贷款合同管理 宏达贷款合同管理系统 v1.0
- shopping-list-modules-day
- psiat1
- Meross:研究Meross MSS310智能插头
- apache-maven-3.6.3-bin
- Eduonix-[removed]JavaScript游乐场,该资源库探索了不同的JS组件,功能以及如何使工具直观