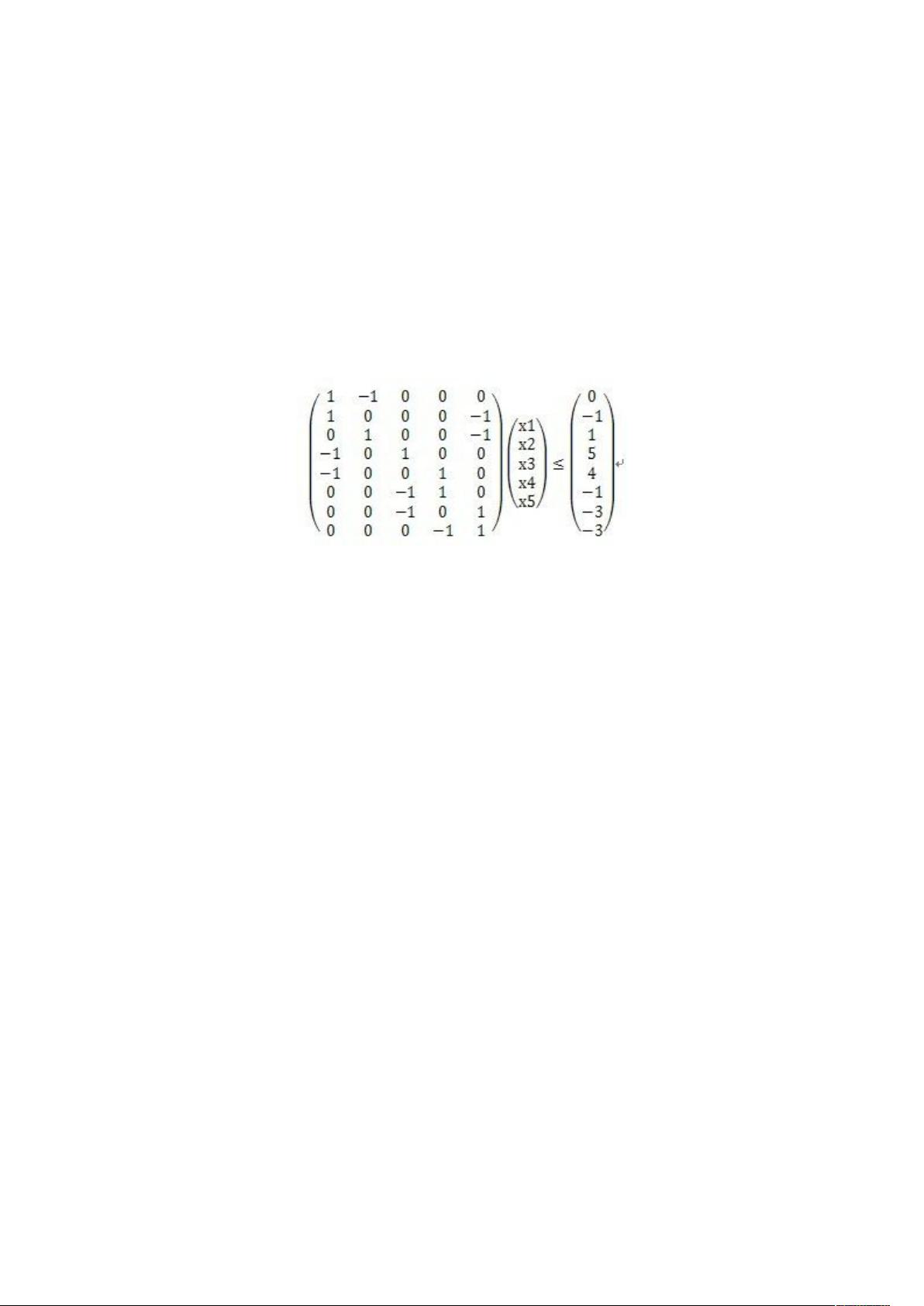差分约束系统深度解析

"差分约束系统是解决一系列线性不等式约束问题的数学模型，主要应用于路径规划、网络流优化等领域。它通过定义变量之间的差异关系来建立约束，每个约束通常表示为一个变量减去另一个变量的差不超过某个常数。在差分约束系统中，线性规划矩阵A具有特定的结构，即每行有一个1，一个-1，其余为0，这对应于不等式的形式：xj - xi ≤ bk。" 差分约束系统的本质在于，它们将复杂的多变量关系简化为变量之间的差异关系，使得问题更易于处理。这种模型可以用来描述许多实际问题，如物流配送中的路径规划，其中每个节点代表一个位置，而约束条件则限制了从一个位置到另一个位置所需的时间或距离。 在上述的示例中，我们有一个五维向量x，需要找到满足特定差分约束的解。这些约束包括了不同维度之间的相对大小关系，例如x1 - x2 ≤ 0表示x1不能大于x2。通过调整这些约束，我们可以找到符合要求的所有可能解。 差分约束系统的解具有一定的性质。引理指出，如果x是系统的一个解，那么x加上任意常数d也是解。这意味着解的空间不是孤立的点，而是一组平行的超平面。这个性质对于理解解的几何特性非常有用。 进一步地，差分约束系统可以转化为约束图，这是一个带权有向图，其中顶点代表变量，边表示约束。边的权重对应于差分约束的右端常数bk。若图中不存在负权回路，那么从顶点v0到其他任何顶点的最短路径长度就构成了一个可行解。这是因为沿着最短路径行走，不会违反任何约束，因为每一步（边）都不会增加路径的权重（总和）。 定理表明，只要差分约束系统的约束图没有负权回路，那么从v0到所有其他顶点的最短路径向量x就是该系统的解。这个定理是差分约束系统求解的关键，因为它提供了一种通过图论算法（如Dijkstra算法或Bellman-Ford算法）寻找解的方法。 差分约束系统是一种强大的工具，用于在满足一组线性不等式约束的情况下寻找变量的解。它可以通过构建约束图并利用图的最短路径算法来求解，这在很多工程和科学问题中有着广泛的应用。理解和掌握差分约束系统及其转化方法，对于解决实际问题，尤其是那些涉及变量之间相对关系的问题，是非常有益的。