线性规划与单纯形法详解：问题建模与求解策略

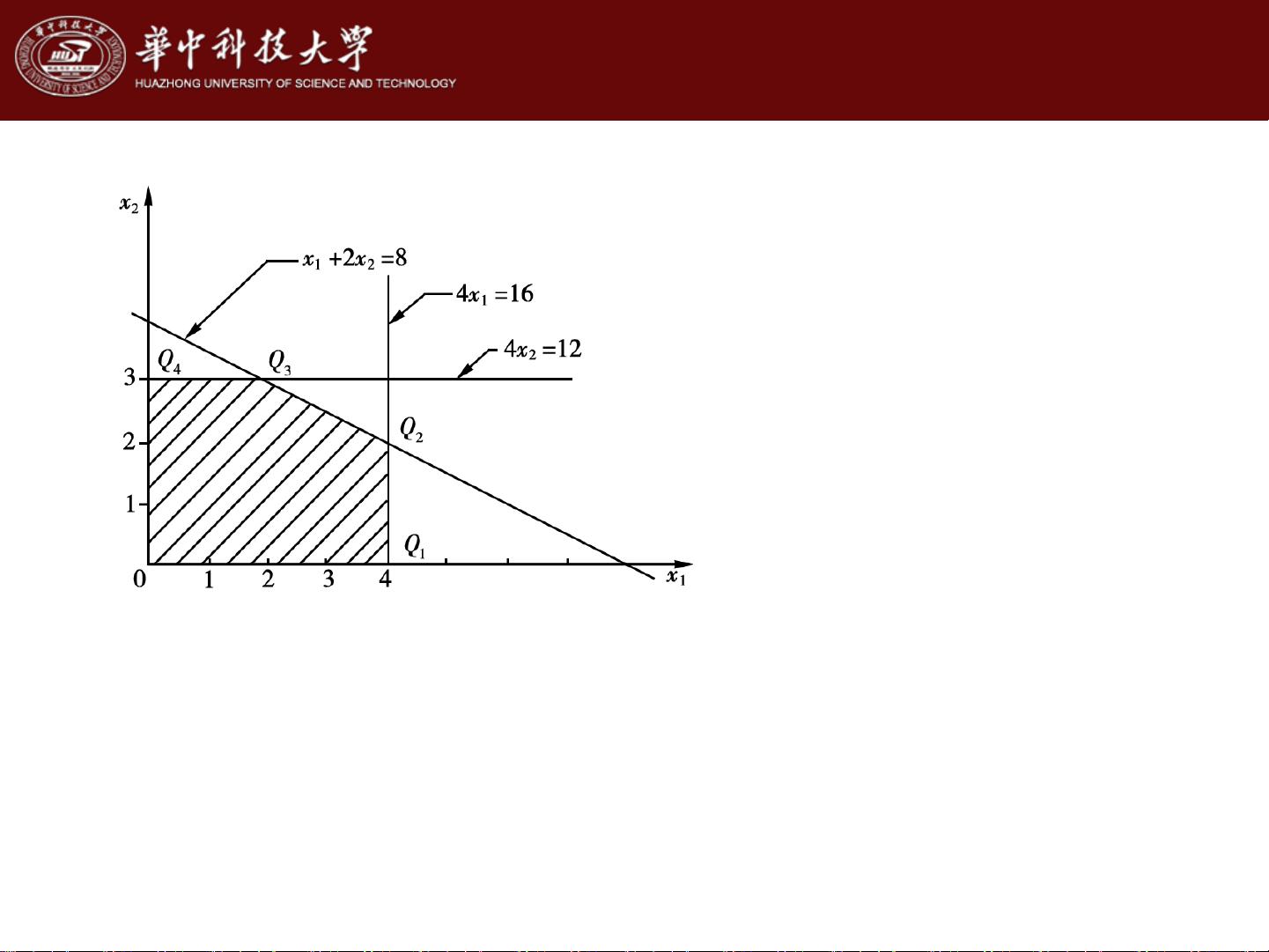
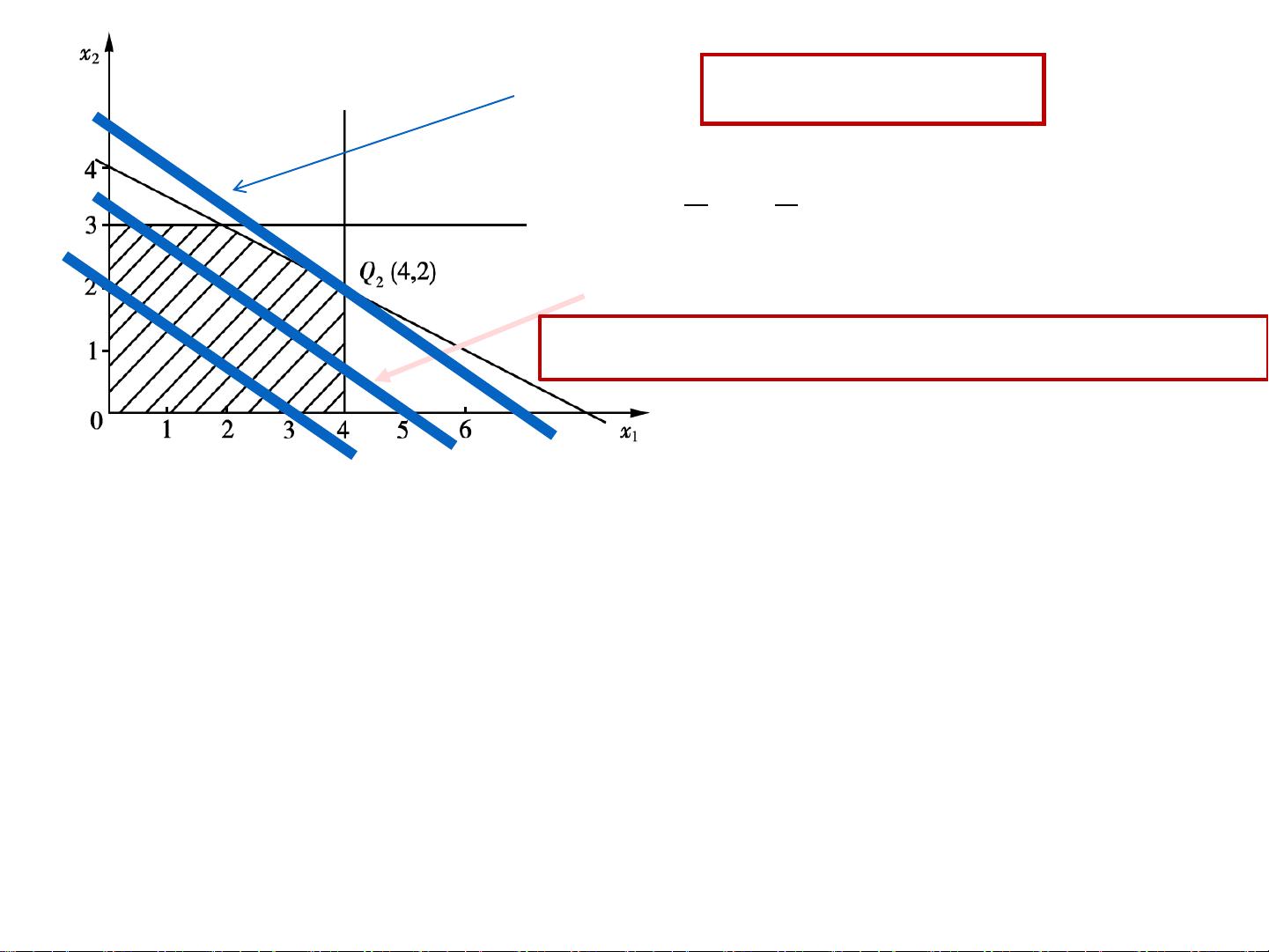
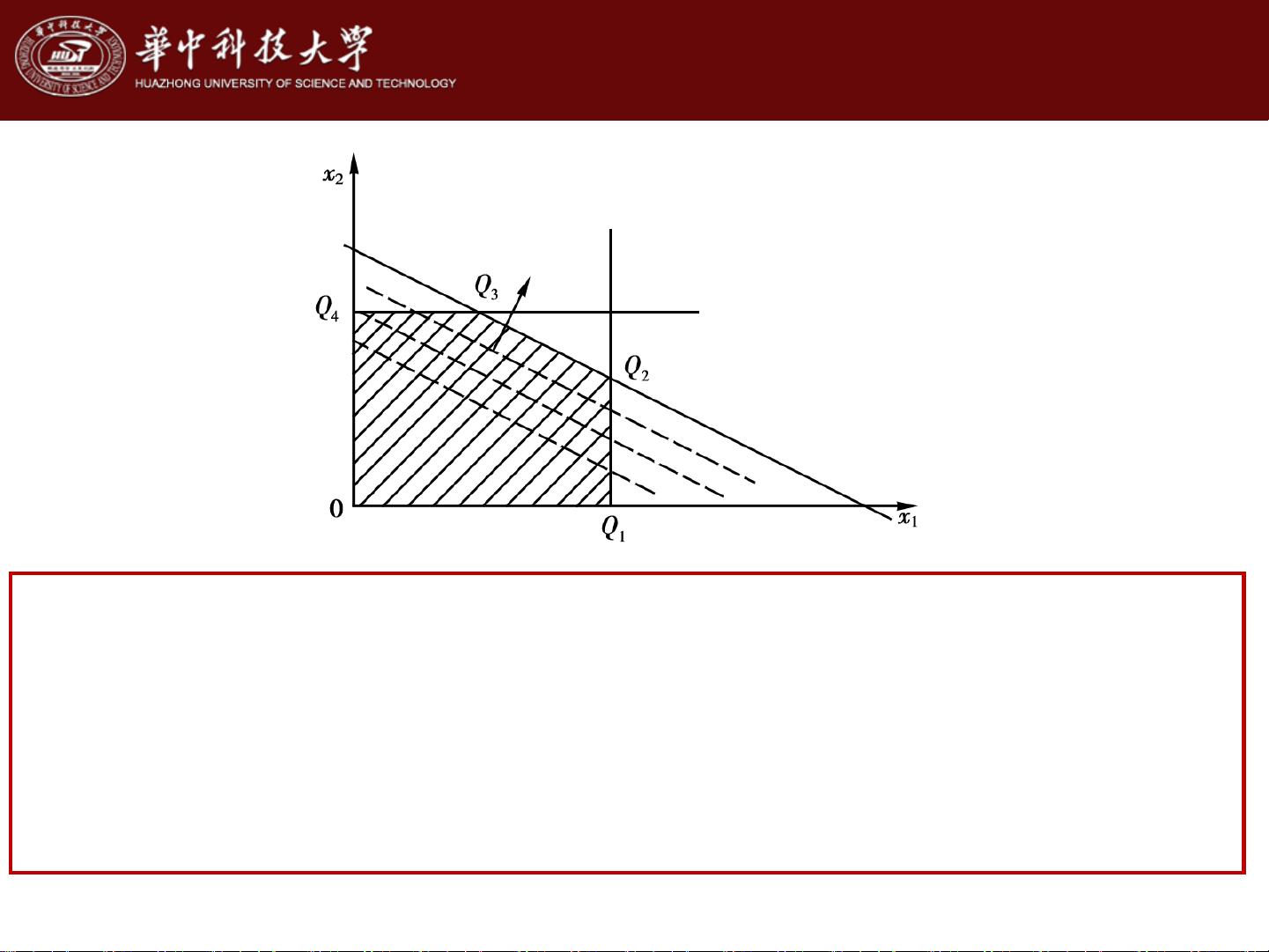
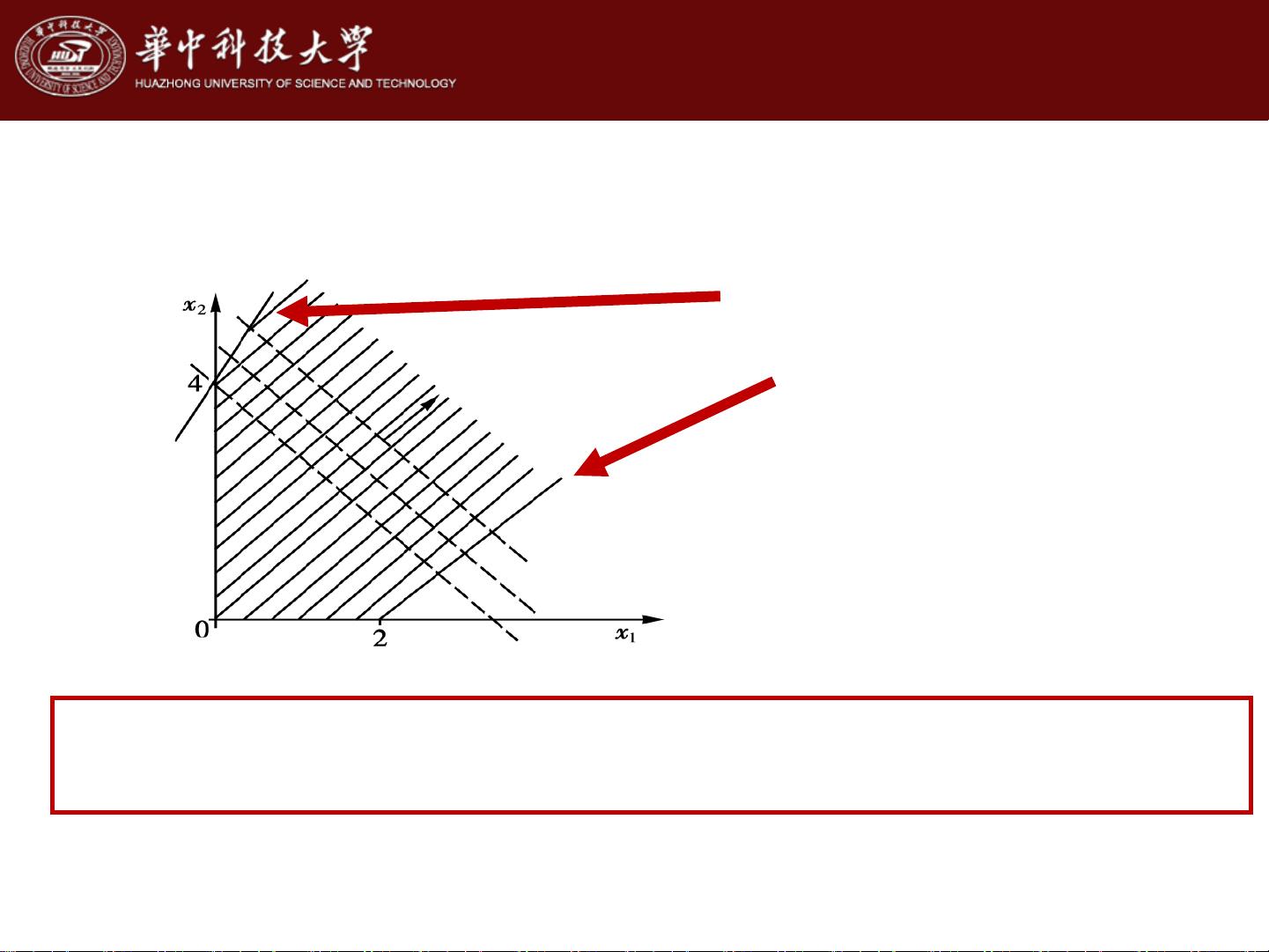
第2章 "线性规划与单纯形法" 是运筹学领域的重要内容，主要针对的是在有限资源条件下优化决策问题。本章由讲师王博，来自人工智能与自动化学院，系统科学与工程系，通过电子邮件wb8517@hust.edu.cn和QQ号2734802827进行教学指导。 第1节"线性规划问题及其数学模型" 开始，介绍了线性规划问题的基本概念。它探讨了如何在实际生产和经济活动中，设定如生产Ⅰ和Ⅱ产品的数量决策变量（如$x_1$和$x_2$），并受到设备、原材料等资源的限制。这些限制形成了约束条件，如$x_1 + 2x_2 \leq 8$，确保资源的有效利用。目标是通过最大化利润函数（如$2x_1 + 3x_2$）来确定最优生产策略。 例1以一个具体工厂为例，说明如何构建线性规划模型，包括设备需求、原材料消耗和利润计算，以及如何将这些因素转化为数学表达式。目标函数和约束条件明确地定义了问题的关键要素。 在第2节"线性规划问题的几何意义"，学习者会理解这些问题是如何通过图形方式表示的，线性约束条件在平面或更高维度空间中的表现，有助于直观地解读问题的结构。 第3节"单纯形法"是解决线性规划问题的一种常用算法，其核心步骤包括选择基变量、计算检验数、移动到下一个可行解直至达到最优解。这一节详细讲解了单纯形法的操作过程，包括如何通过迭代更新来优化生产计划。 第4节深入探讨了单纯形法的计算步骤，可能涉及如何确定起始基、如何执行换基操作，以及如何判断是否达到最优解的终止条件。 第5节"单纯形法的进一步讨论"可能涵盖了单纯形法的局限性、优化效率分析以及与其他优化方法（如图解法）的比较。 第6节"应用举例"通过实际案例，如简化环境保护问题，展示了线性规划在解决实际问题中的应用场景，比如工业污水处理中的合理分配问题。 第2章线性规划与单纯形法章节提供了理论基础和实践技巧，对于理解和解决现实生活中的多目标优化问题具有重要意义。学习者通过深入理解这些内容，能够掌握如何在有限资源约束下做出最佳决策，提升决策制定和优化的能力。