解析信号处理：傅里叶变换连接时频域

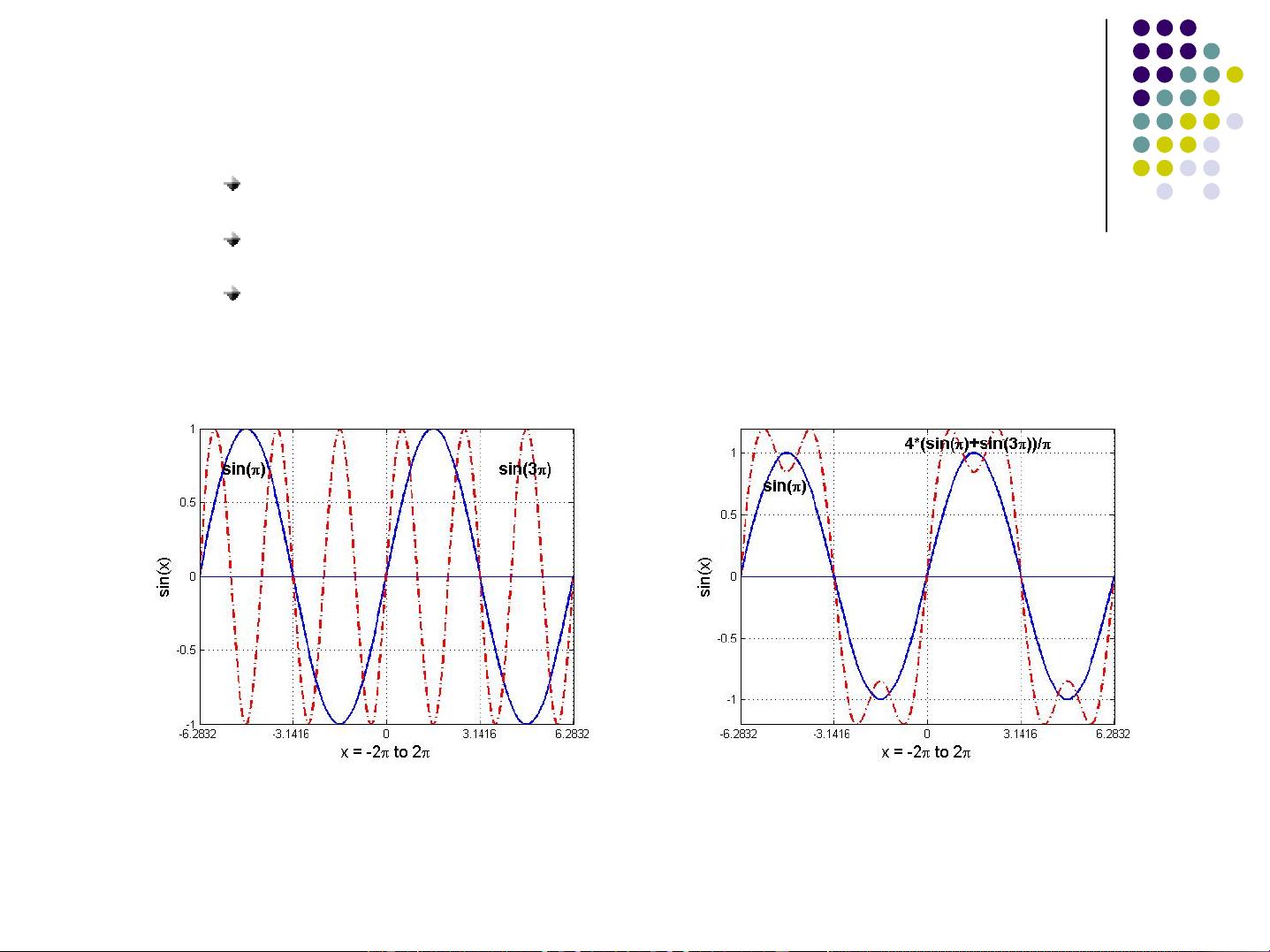
傅里叶变换是信号处理领域的重要工具，它将时间域和频率域这两个看似不同的概念连接起来，提供了深入理解并操作复杂信号的强大手段。傅里叶分析源于法国数学家让-巴蒂斯特·傅里叶的工作，尽管他未能成为炮兵军官，但他的理论对科学和技术产生了深远影响。 傅里叶变换的重要性主要体现在以下几个方面： 1. **信号解析与分析**：通过傅里叶变换，可以将一个复杂的时域信号分解为一系列正弦或余弦波的线性组合，这些基本频率成分揭示了信号的本质特征，如音乐中的音调、图像中的色彩频率等。 2. **计算效率提升**：在时域进行信号处理可能涉及大量的运算，特别是在处理大量数据时。傅里叶变换允许我们把问题转化为频域，许多计算操作变得更简单，例如滤波、频谱分析等，这大大节省了计算资源。 3. **简化模型和设计**：在频域中，信号的特性更容易理解和设计。比如，我们可以设计特定的滤波器只保留某些频率成分，或者去除不需要的噪声，这对于信号处理系统的设计非常关键。 4. **声学应用示例**：傅里叶变换在音频处理中举足轻重。如上文所述，通过对声音信号进行傅里叶变换，我们可以确定其包含的频率成分，如一个声音由50Hz和120Hz的频率混合而成，并识别出其他噪音。 5. **三角函数基础**：傅里叶变换涉及到三角函数，如正弦和余弦函数，它们构成了傅里叶级数的基础。周期性函数的性质在傅里叶分析中扮演着核心角色，因为许多实际信号都是周期性的。 6. **离散傅里叶变换（DFT）和快速傅里叶变换（FFT）**：为了处理数字信号，我们通常使用离散版本的傅里叶变换，而快速傅里叶变换（FFT）则是DFT的一种高效算法，显著减少了计算时间，尤其在大数据集上。 7. **二维傅里叶变换（2D FFT）**：对于二维信号，如图像，傅里叶变换扩展到了两个维度，用于分析图像的频率分布，如颜色和纹理特征，这在图像处理、计算机视觉等领域广泛应用。 傅里叶变换作为信号处理的基石，通过在时间域和频率域之间建立桥梁，使得我们在处理信号时能够采取更高效的方法，洞察信号的内在结构，从而优化设计和分析过程。无论是音频分析、通信工程、图像处理还是信号处理的众多分支，傅里叶变换都发挥着至关重要的作用。