数字图像处理：正交变换与离散傅里叶分析

"北京邮电数字图像处理第三章ppt涵盖了图像的变换，包括空间域处理法和变换域处理法，重点介绍了图像变换的条件、正交变换、离散傅里叶变换（DFT）、离散余弦变换（DCT）、沃尔什变换和哈达玛变换以及离散小波变换（DWT）。" 在数字图像处理领域，图像变换是不可或缺的技术，其目的是为了更好地理解和处理图像。图像变换主要有两种方法：空间域处理法和变换域处理法。空间域法直接对图像像素进行操作，而变换域法则通过对图像进行数学变换，将其转换到不同的表示域，便于分析和处理。 图像变换需满足三个主要条件：可逆性、有利于进一步运算以及算法简单。可逆性确保原始信息的保留，通过逆变换能恢复原图像；变换后应能突出图像的特征或简化数据处理；快速的算法可以提高处理效率，尤其是对于大型图像，矩阵运算速度至关重要。 正交变换是图像处理中的关键工具，它包括正弦型变换和方波型变换，如傅里叶变换、余弦变换、沃尔什变换和哈达玛变换等。正交变换的原理基于正交矩阵，使得变换前后矩阵乘积为单位矩阵，保证了可逆性。正交变换在图像增强、复原、编码、描述和特征提取等多个方面都有广泛应用。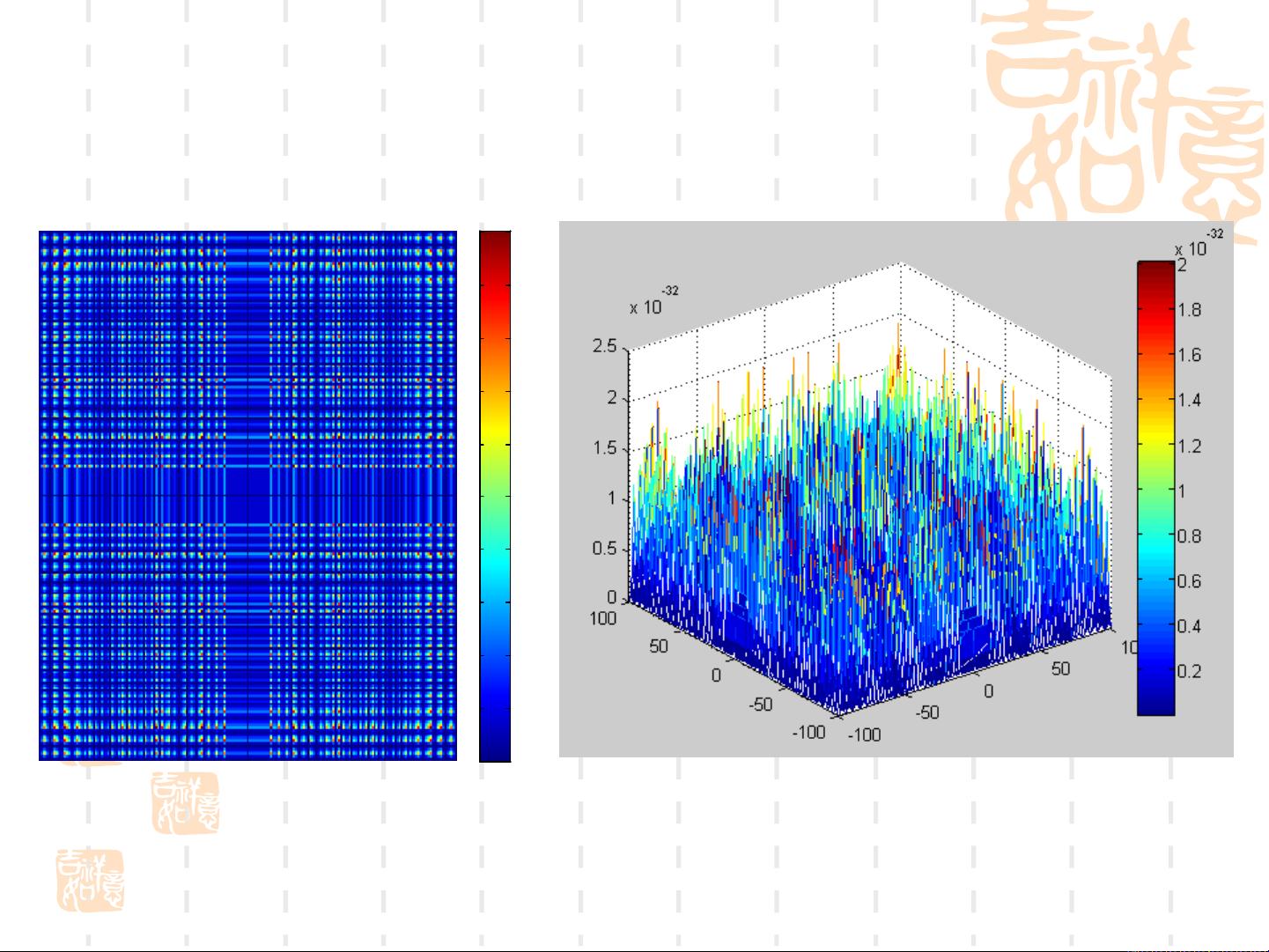 离散傅里叶变换（DFT）是数字图像处理中的核心变换之一，它扩展了连续傅里叶变换的概念，用于处理离散信号。DFT将图像从空间域转换到频率域，揭示了图像的频谱信息，这对于滤波、压缩和分析图像的高频或低频成分非常有用。 离散余弦变换（DCT）是另一种常用的图像变换，尤其在图像压缩领域，如JPEG格式，DCT能有效地捕捉图像的主要视觉信息，同时去除冗余数据。 沃尔什变换和哈达玛变换属于方波型变换，它们在图像处理中提供了另一种表示方式，对于二值图像和特定类型的信号处理有优势。 离散小波变换（DWT）是一种多分辨率分析方法，能够同时获取图像的空间和频率信息，适用于图像的细节提取和噪声分离。 这些变换在实际应用中各有优势，选择哪种变换取决于具体任务的需求。理解并掌握这些变换对于深入研究数字图像处理和相关应用至关重要。