同步时序电路设计：状态表化简方法解析

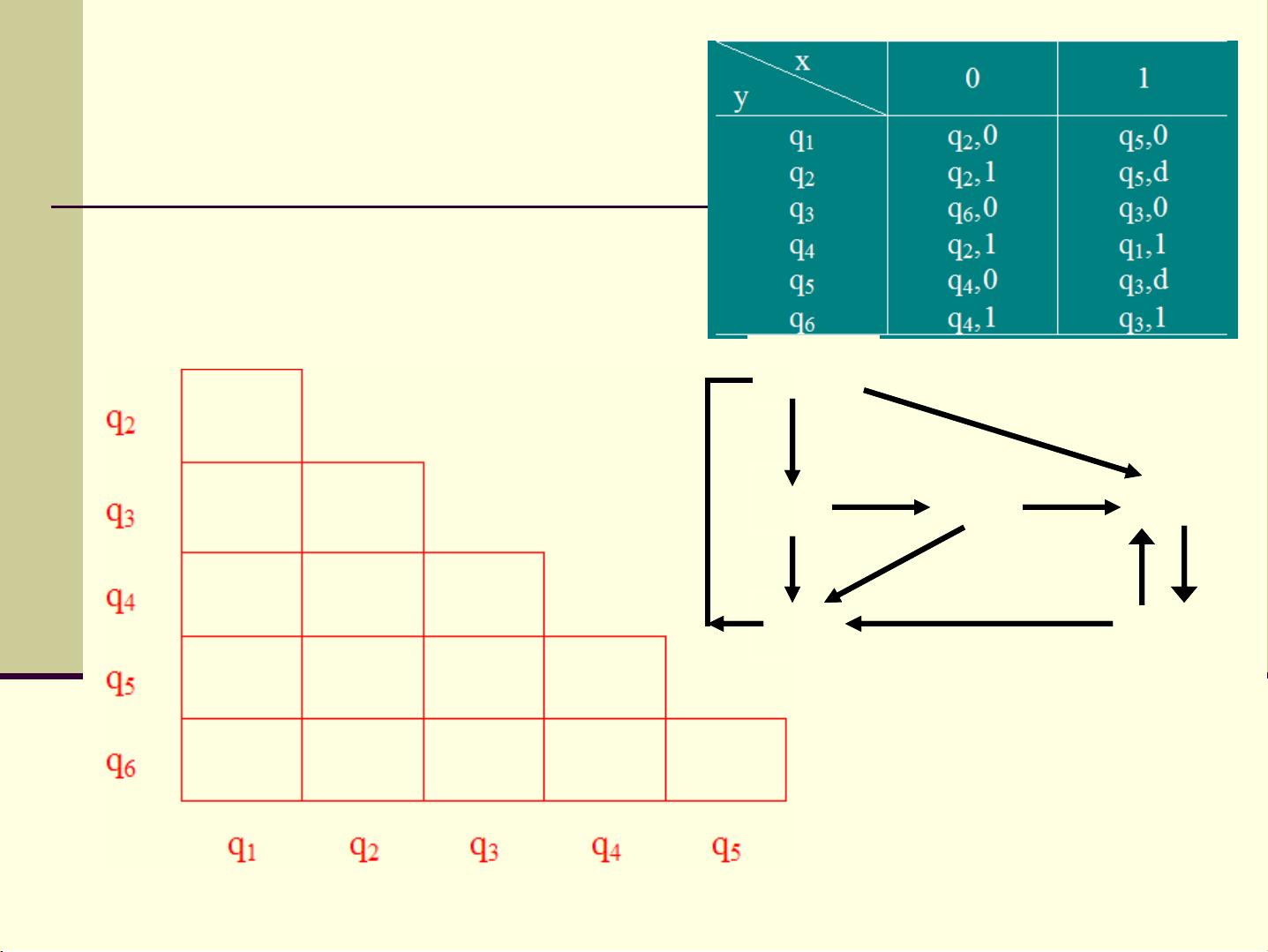
"国防科学技术大学计算机系体系结构教研室的数字逻辑与工程设计PDF课件，专注于同步时序电路的设计，特别是状态表的化简方法。" 本文主要讲解了同步时序逻辑电路的设计，其中核心内容是关于状态表的化简，特别是针对不完全定义机状态表的处理。同步时序电路是一种重要的数字电路类型，它的行为由当前状态和输入信号共同决定，且状态转换是同步于时钟信号的。 在介绍中提到了"相容"这一概念，相容状态是指在不完全定义机状态表中，如果两个状态的输出和次态在它们都有定义的情况下满足合并条件，那么这两个状态就是相容的。例如，状态A和B、B和C是相容的，而A和C则不是。值得注意的是，相容状态并不具有传递性，即相容状态对(A,B)和(B,C)并不意味着(A,C)也一定是相容的。 为了寻找最大相容类，文章提出了"合并图法"。通过构建相容状态对和相容类，可以找到那些能够相互合并而不违反相容性的状态集合。例如，相容状态对(q1,q2),(q1,q3),(q1,q4),(q2,q4),(q3,q4)可以形成相容类(q1,q2,q4)和(q1,q3,q4)。 接下来，文章介绍了化简状态表的步骤，主要分为三个步骤： 1. **隐含表法**：首先绘制隐含表，通过比较不同状态的输出和次态来标记相容状态对。如果状态的输出（除去随意项）不相同，则标记为"×"；如果输出相同且次态满足相容条件，标记为"√"；若输出相同但次态关系不确定，则填写次态对以供后续分析。 2. **状态合并图**：基于隐含表，构造状态合并图，目的是找出最大相容类。这涉及到寻找那些能够覆盖原始状态表所有状态，且数量最少的相容类组合，同时确保这些相容类在所有输入下产生的次态仍属于该组。 3. **最小化状态表**：最后，根据覆盖性、最小性和闭合性这三个条件，确认化简后的状态表是否有效。覆盖性意味着化简后状态需要覆盖所有原始状态，最小性指化简状态的个数尽可能少，闭合性则确保每个状态在任何输入下都能转移到同一组内的其他状态。 通过这样的方法，可以有效地简化同步时序电路的状态表，从而减少电路的复杂度，提高设计的效率和实现的可行性。例如，课件中给出的实例展示了如何通过这些步骤对原始状态表进行化简，以找到最小化且满足条件的状态表示。这种化简过程对于理解和设计复杂的数字系统，如微处理器、存储器控制器等，至关重要。