参数三次样条曲线曲面：CAGD中的高效几何设计

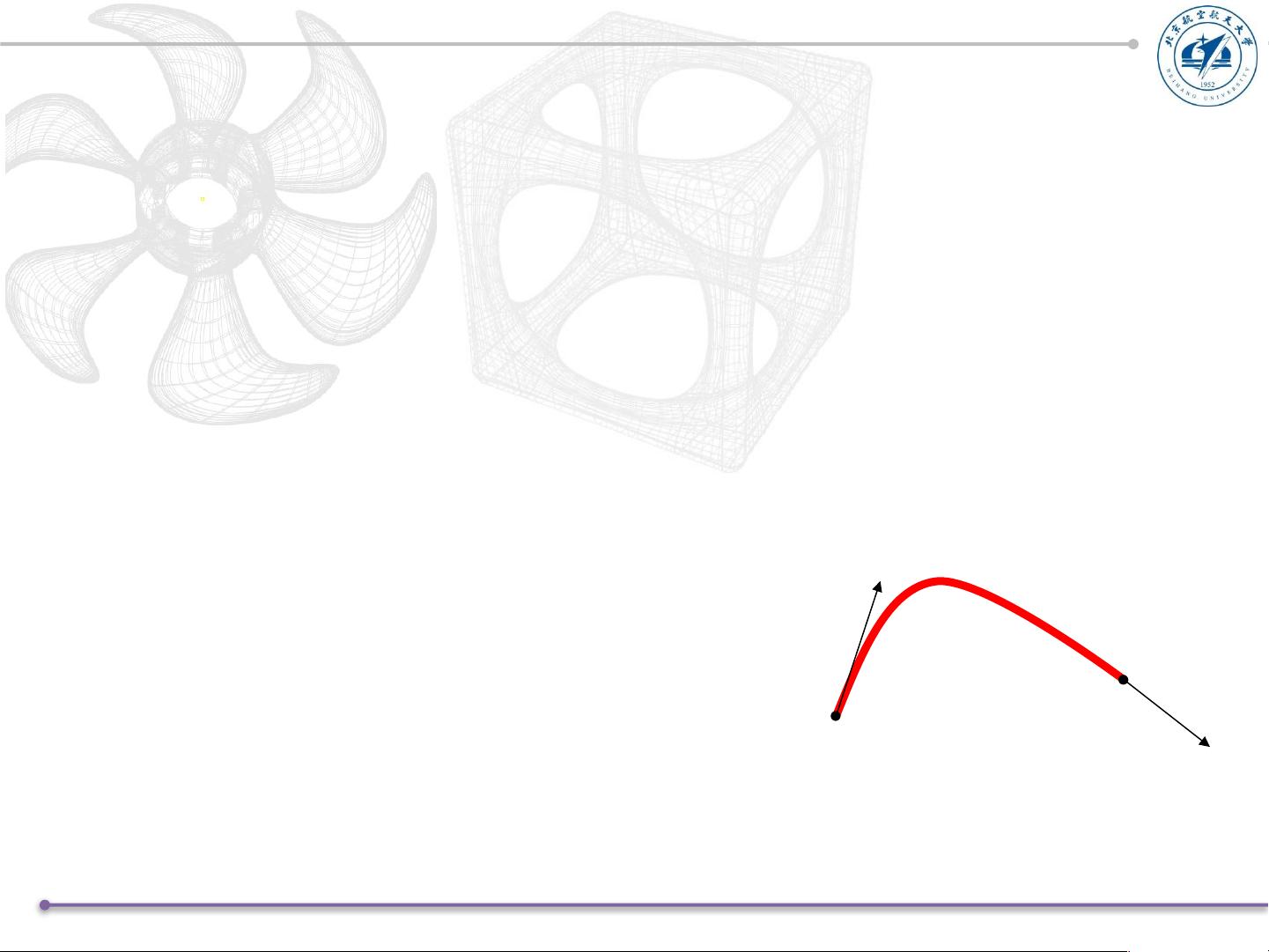
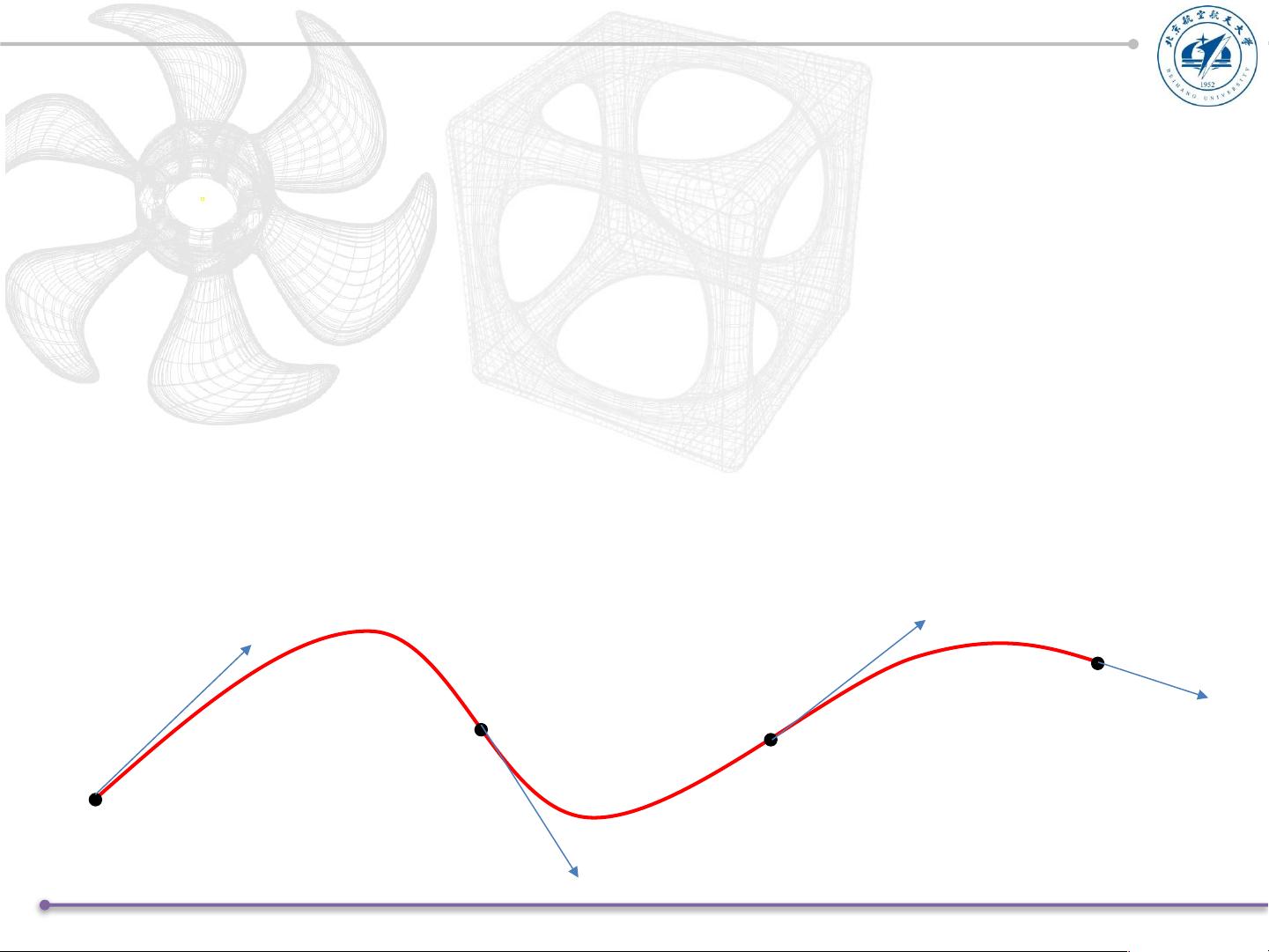
CAD几何运算的核心是参数样条曲线曲面技术，这是一种在计算机辅助几何设计(CAGD)中广泛应用的方法。参数样条曲线曲面的构建旨在提供一种高效且灵活的方式来表达复杂的几何形状，同时满足C2连续性的需求，即曲率连续，使得图形平滑无突兀。 参数多项式插值是基础，特别是在设计过程中，它允许通过一系列的参数控制曲线的形状。其中，参数三次样条曲线曲面是一种特别重要的类型，它结合了三次多项式函数的简单性和控制性。这种曲线由一组特定的参数定义，每个参数对应一个特定的权重，这些权重决定了曲线在各个插值点附近的形状。 北京航空航天大学机械工程及自动化学院的研究人员杨佳明、吴佳力、郭有章和蒋振邦在其工作中，对参数三次样条曲线曲面进行了深入探讨。他们首先回顾了曲线的矢函数表示法，其中系数矢量是关键，通常基于预设的约束条件，如插值点或逼近点，这些条件决定了曲线的具体形状。 然而，传统的多项式插值方法如幂基、拉格朗日基和埃尔米特基存在一些局限性。比如，随着插值条件的增加，多项式的次数增高，可能导致曲线出现扭摆现象，而且计算复杂度也随之上升。此外，高次多项式插值并不总是收敛的，尤其是在加密数据点时，可能会导致发散。另外，系数矢量的含义和控制性在传统形式下可能不够直观。 为了克服这些问题，研究者引入了组合曲线的概念，通过组合多个参数样条段来构建更复杂但连续的曲线。Ferguson参数三次曲线是其中的一种优化方法，它可能提供了更好的曲线控制和性能，使得设计师能够更容易地实现所需的设计精度和灵活性。 CAD几何运算的核心是参数样条曲线曲面技术，特别是参数三次样条，它不仅简化了复杂曲线的建模过程，还确保了几何连续性，对于航空航天等领域的设计和制造有着重要的应用价值。通过不断优化和改进算法，这种技术正在推动CAD技术的进步。