探索离散时间傅里叶变换：MATLAB实验与信号分析关键

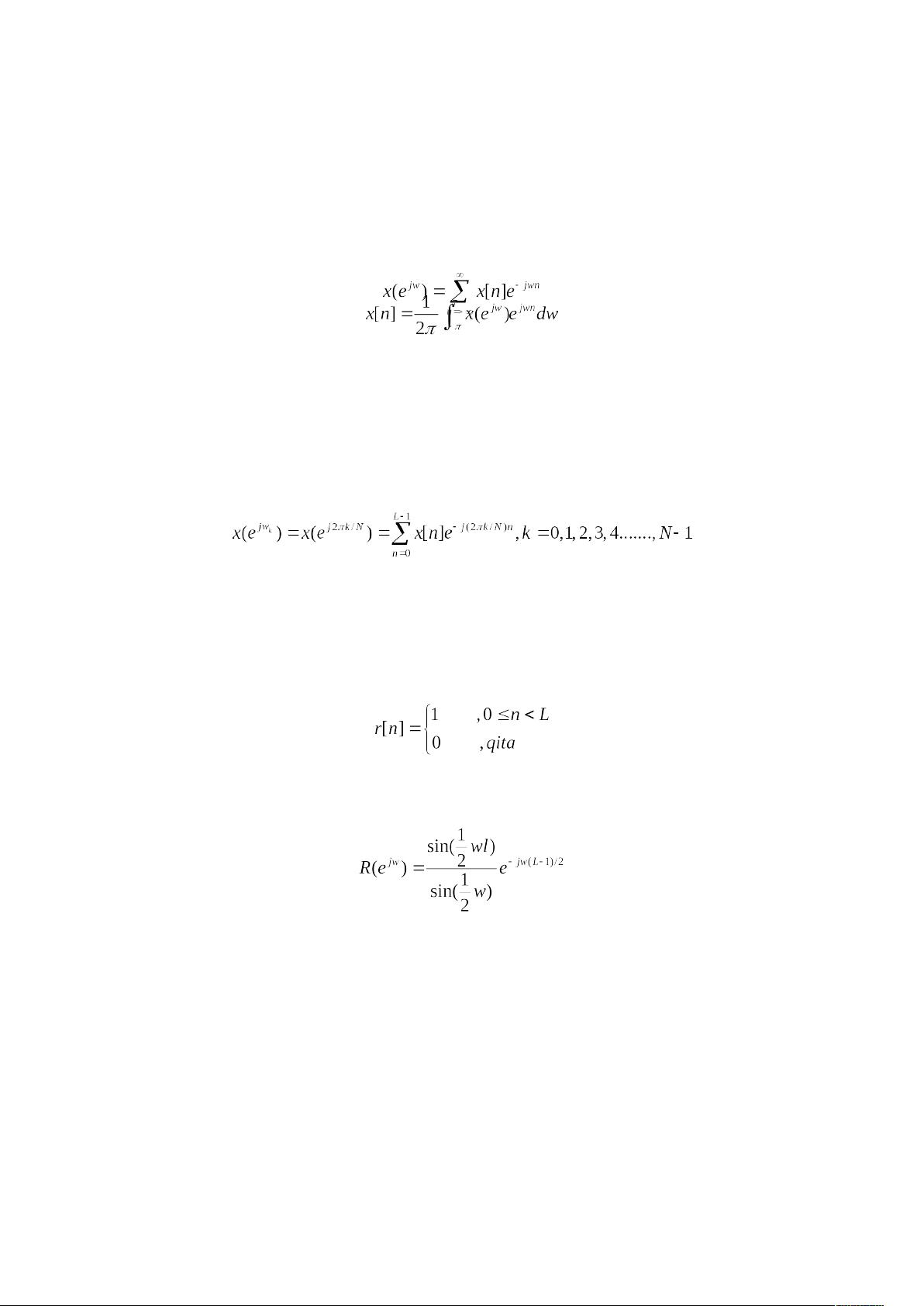
本篇实验主要围绕离散时间傅里叶变换（DTFT）展开，这是数字信号处理中的核心概念，用于信号分析和滤波设计。实验分为两大部分：理论理解和实践操作。 首先，实验原理部分介绍了离散时间正逆傅里叶变换（DTFT）在信号分析中的关键作用。DTFT是连续时间傅里叶变换在离散时间序列中的等价物，它将离散信号转化为频率域的描述，频率响应提供了LTI系统行为的直观理解。由于MATLAB处理的是有限长度信号，所以通常选取周期为2π的有限区间，如[-π, π)或[0, π)，并利用均匀抽样计算离散傅立叶变换（DFT）。 接下来的实验内容包括具体操作： 1. 实验对象是矩形脉冲r[n]，通过公式定义。要求编写MATLAB函数asinc(w, L)，直接计算在给定频率网格上的asinc函数，然后绘制该脉冲信号的DTFT并与DFT结果对比。这有助于理解和应用DTFT的实际计算过程。 2. 对于指数信号x[n] = (0.9)^u[n]，首先利用freqz函数计算其DTFT的幅度和相位特性。实验要求观察并解释幅度特性为何是w的偶函数，相位特性为何是w的奇函数。这涉及到信号的周期性和对称性在频域的表现。 3. 实践环节进一步深化，通过推导一阶系统幅度和相位特性的表达式，然后用这些理论公式计算出幅度和相位特性，并与freqz函数的结果进行对比，检验理论与实际计算的一致性。 实验程序部分展示了如何运用MATLAB的特定函数和命令，如formatcompact、subplot、dtft、freqz等进行DTFT的计算和可视化，以及如何处理信号的频谱特性。 总结来说，这个实验涵盖了离散时间傅里叶变换的基础理论、计算技巧以及实际应用，不仅锻炼了学生对DTFT的理解，还提高了他们使用MATLAB进行信号处理的能力。通过实验，学生能够深入理解信号在时域和频域的转换，以及不同信号特性在DTFT中的体现。