机器学习基础：线性回归与梯度下降详解

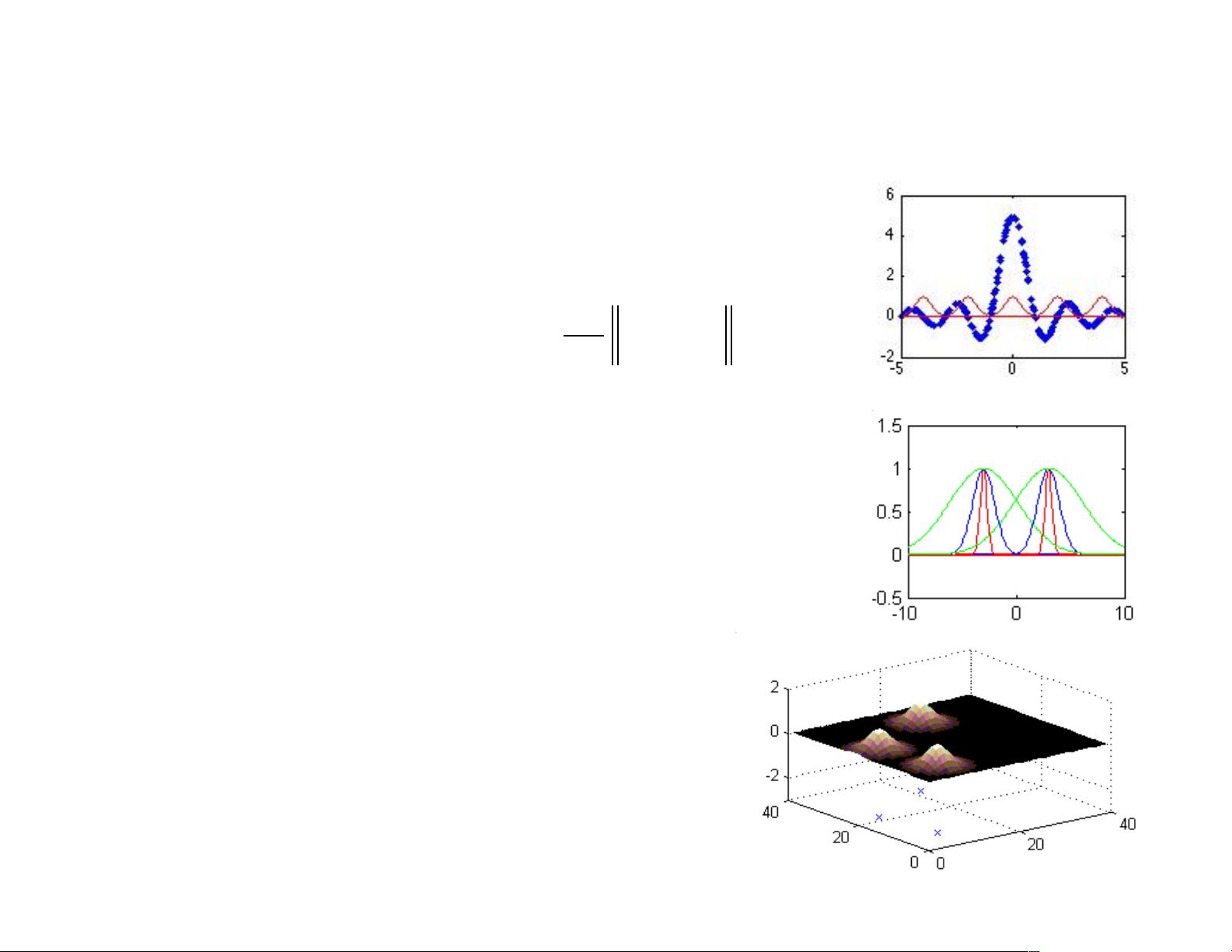
在"Class3x.pdf"中，该文档深入探讨了机器学习的基本概念，特别关注哥伦比亚大学教授Tony Jebara的课程。内容涵盖了线性回归、分类方法以及模型复杂度的理解。以下是对这些主题的详细解读： 1. **Additive Models and Linear Regression**: 这部分介绍了线性回归作为机器学习中的基础算法，它通过建立输入特征与目标变量之间的线性关系来预测结果。线性模型简单易懂，但可能不足以捕捉数据中的复杂模式，特别是当数据存在非线性关系时。 2. **Sinusoids and Radial Basis Functions**: 文档提到，除了线性函数，我们还可以使用更复杂的基函数，如正弦函数，它们能够模拟周期性的行为。另外，radial basis functions（RBF）是一种常用的非线性函数族，它们根据输入特征的欧氏距离来定义函数值，适用于多维空间中的非线性建模。 3. **Classification**: 进入到分类问题，文档提到了逻辑回归（Logistic Regression），这是一种广泛用于二分类问题的算法。它通过将线性函数转换为概率形式，使得输出值可以被解释为类别的可能性，适合于处理线性和可分离的数据。 4. **Gradient Descent**: 梯度下降法是优化算法的核心，用于找到函数的最小值，这对于训练线性和非线性模型至关重要。它通过迭代地沿着函数梯度的反方向调整参数，直到达到局部最优解。在文档中，它详细介绍了如何应用梯度下降求解线性回归和分类问题中的最小损失函数。 5. **Polynomial Basis Functions**: 文档展示了如何使用多项式函数扩展线性模型，例如对于多变量数据，可以组合不同阶的特征交叉项来捕捉潜在的非线性模式。这在处理非线性关系时非常有用，尤其是在处理二次及以上阶的交互效应时。 6. **Tikhonov Regularization (欠饱和与过饱和)**: 文档提到了欠饱和（underfitting）和过饱和（overfitting）的概念，这是在选择模型复杂度时需注意的问题。欠饱和模型过于简单，无法很好地拟合数据；而过饱和模型过于复杂，可能会过度拟合训练数据，导致在新数据上的表现不佳。理解何时使用高阶多项式或更简单的模型至关重要。 7. **Additive Models与Non-polynomial Basis Functions**: 除了多项式函数，文档强调了更为一般的加性模型，允许使用任何类型的基函数，这为模型选择提供了更大的灵活性。这包括但不限于正弦函数和其他数学函数，这些函数能够更好地适应数据的特定特性。 "Class3x.pdf"是一份全面的机器学习教程，深入探讨了线性模型及其扩展，以及如何通过梯度下降法进行参数优化，同时强调了模型选择和复杂度控制的重要性。这对于理解和应用机器学习的基础理论和技术具有很高的参考价值。