使用双线性变换法设计IIR带通滤波器及MATLAB仿真

"基于双线性变换法的带通滤波器设计，通过MATLAB进行仿真，用于设计IIR数字巴特沃思滤波器，重点关注滤波器的通带和阻带截止频率以及衰减指标。" 在信号处理领域，设计滤波器是一项关键任务，特别是对于数字信号处理系统。本文主要探讨的是基于双线性变换法的IIR（无限 impulse response）数字巴特沃思带通滤波器设计。这种方法允许将模拟滤波器转换为数字滤波器，同时保持其频率特性。 双线性变换法是一种常用的模拟到数字滤波器转换技术，它能够保持滤波器的线性和时不变性。在这个例子中，设计的目标是创建一个具有特定通带和阻带截止频率的滤波器，同时满足给定的衰减指标。通带截止频率wp11和wp12分别设定为2.3 kHz和4.55 kHz，阻带截止频率ws11和ws12设定为0.8 kHz和6.05 kHz。此外，Ap和As定义了通带和阻带的衰减，分别为1dB和40dB，这会影响滤波器对不同频率信号的响应。 首先，通过数字频率wp1和wp2与采样频率Fs的关系计算出模拟频率Wp1和Wp2。接着，确定模拟滤波器的指标，包括转换为模拟带通滤波器所需的零点和极点。这里使用了MATLAB函数`buttord`来计算滤波器的阶数n，以及相应的截止频率Wn，确保满足给定的通阻带衰减指标。 之后，使用`buttap`函数设计一个n阶模拟低通巴特沃思滤波器，并通过`zp2tf`将其转换为零极点形式。然后，借助`lp2bp`函数将这个低通滤波器转换为带通滤波器。最后，运用双线性变换法，即`bilinear`函数，将模拟带通滤波器转换为数字滤波器，得到系数b和a。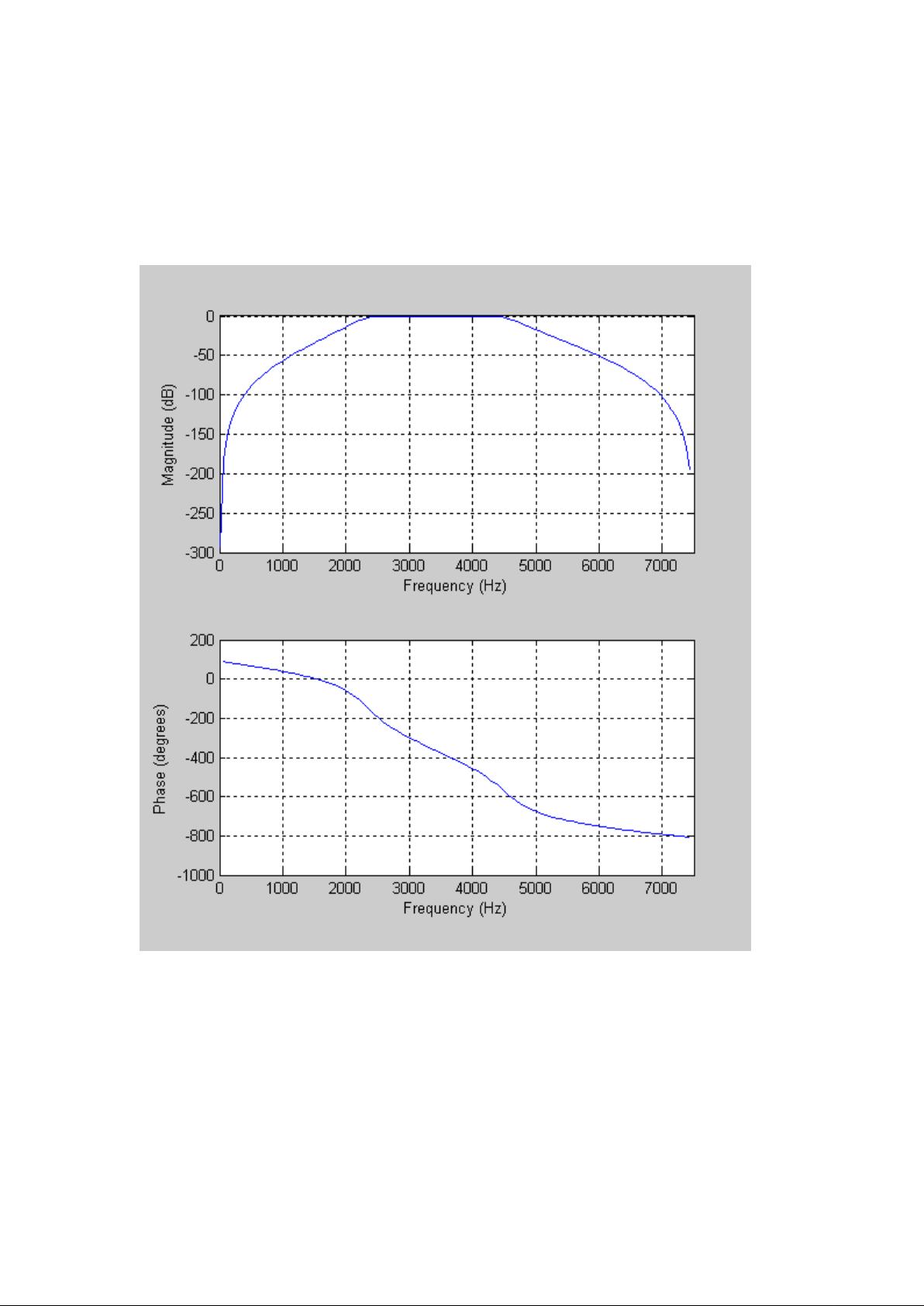 为了验证滤波器的设计，使用`freqz`函数计算了数字滤波器的频率响应，并绘制了相应的图形。此外，还模拟了一个包含三个频率成分的输入信号（1 kHz、2.5 kHz和0 Hz），通过滤波器后，只保留了1 kHz和2.5 kHz的成分，而0 kHz（直流分量）被有效地去除，证明了滤波器的有效性。 这个设计展示了如何使用MATLAB和双线性变换法来实现一个定制的IIR数字巴特沃思带通滤波器，该滤波器可以有效地筛选出特定频率范围内的信号，对于信号分析和处理应用具有重要的实用价值。