二维空间中的可视性算法概览

4星 · 超过85%的资源 | 下载需积分: 9 | PDF格式 | 2.49MB | 更新于2024-08-01 | 105 浏览量 | 举报

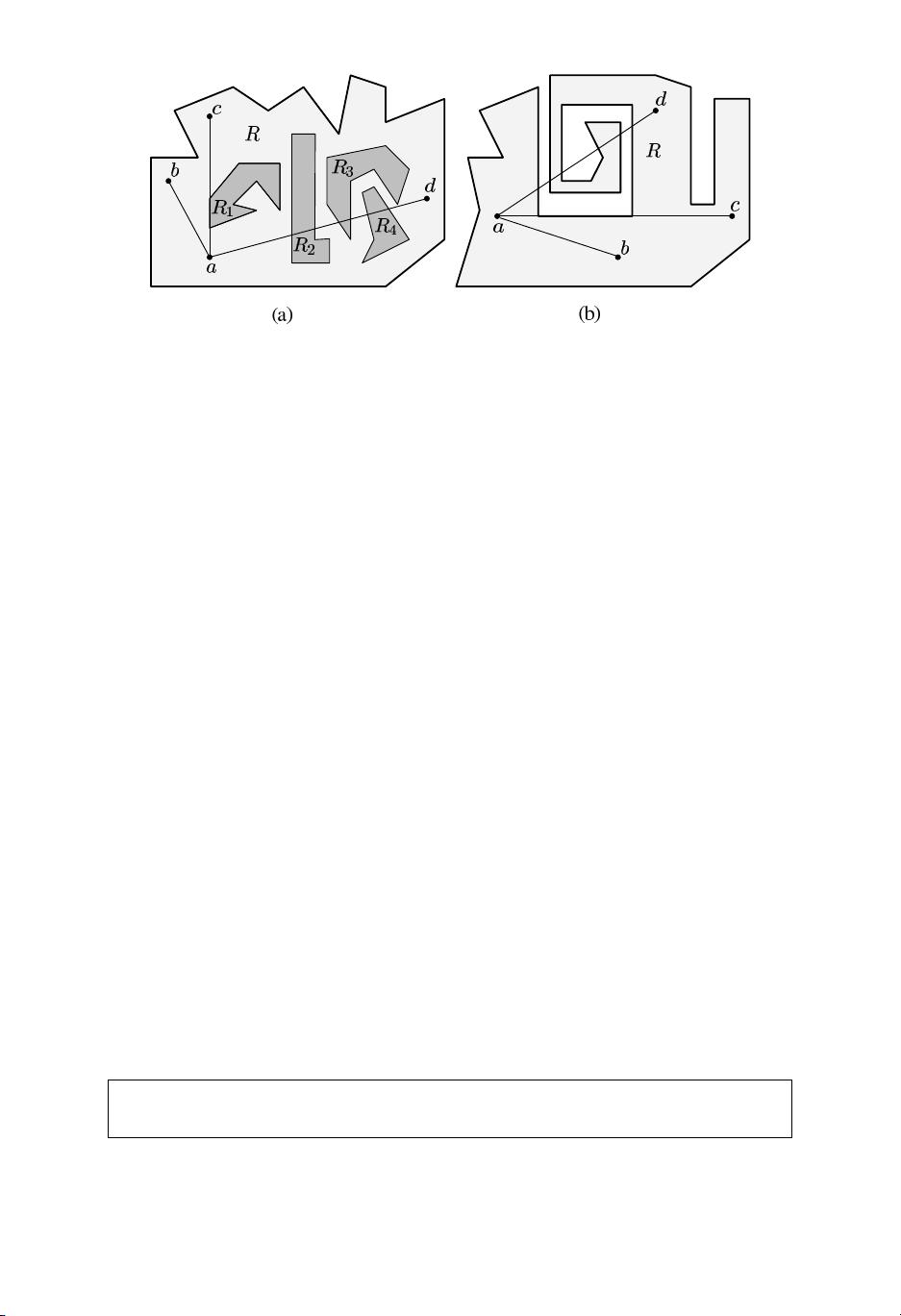
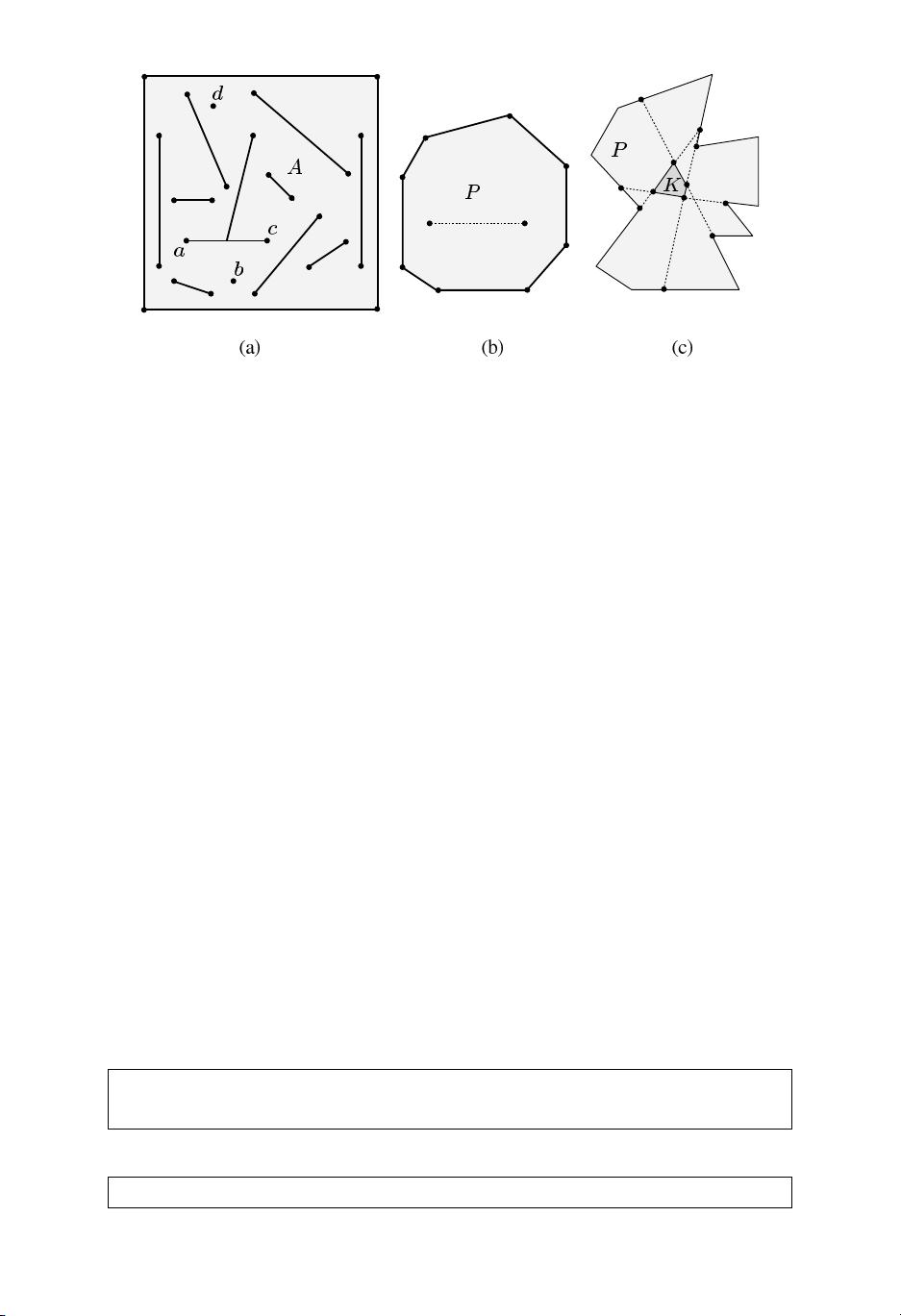
"《平面中的可见性算法》是一本深入探讨二维空间中可见性问题解决方法的书籍。书中涵盖了从简单多边形到带有洞的多边形的各种可见性算法，包括点可见性、弱可见性、最短路径、可见性图理论、链接路径以及路径查询等相关主题。全书包含超过300个图表和数百个练习题，适合计算机图形学、计算几何、机器人学以及几何图论领域的研究生和研究人员阅读，也可作为相关领域研究者的参考书。作者Subir Kumar Ghosh是计算机科学领域的教授。" 本书首先介绍了可见性的基本概念，包括对可见性的定义、多边形的分类、渐近复杂度分析、三角剖分以及艺术画廊问题。接着，详细阐述了点可见性问题，包括在简单多边形和有孔多边形中计算点的可见性，并提出了线性时间复杂度的算法。此外，还讨论了识别从一点可见的简单多边形的方法。接下来，作者探讨了弱可见性和最短路径问题。弱可见性是指视线可以部分穿过物体，而不会被完全阻挡。书中提到了弱可见性的特征、计算简单多边形中弱可见性以及有孔多边形中弱可见性的算法。同时，还介绍了如何构建最短路径树，并讨论了在不同类型的可见性多边形中计算最短路径的方法。 LR-可见性（Left-Right可见性）是另一个重要的主题，它涉及视线从左到右的连续可见性。书中详细描述了LR-可见性的特性，以及如何在LR-可见性多边形中行走和计算最短路径。此外，还讲解了利用LR-可见性计算最短路径树的算法。可见性图是表示物体间可视关系的图论工具。书中介绍了如何构建简单多边形和有孔多边形的可见性图，以及最坏情况和输出敏感的算法。此外，还讨论了凸孔和非凸孔的切线可见性图的计算。在可见性图理论部分，书中研究了识别简单多边形的可见性图的必要条件和测试方法，以及特殊类别的可见性图的特征。此外，还涉及了一些顶点-边可见性图的性质，以及最大团和最大隐藏顶点集的计算。链接路径是另一种形式的路径，它允许视线部分被物体遮挡。书中讲述了如何在简单和有孔多边形中找到最小链接路径，并计算链接中心和半径。此外，还讨论了在凸多边形和非凸多边形之间找到最小嵌套多边形的方法。最后，路径查询部分涵盖了射线射击查询、点在多边形内的可见性查询，以及在简单多边形内两点间的最短路径和链接路径查询。这些查询算法的时间复杂度在不同情况下有所不同。《平面中的可见性算法》提供了丰富的理论知识和实用算法，对于理解并解决二维空间中的复杂可见性问题具有很高的价值。无论是学术研究还是实际应用，这本书都提供了一个全面且深入的资源。

展开

Background

1.1 Notion of Visibility

Visibility is a natural phenomenon in everyday life. We see objects around us and

then decide our movement accordingly. Seeing an object means identifying the

portions of the object visible from the current position of an observer. The entire

object may not be visible as some of its parts may be hidden from the observer. The

observer also determines shapes and sizes of visible portions of an object. Visible

portions of an object change as the observer moves from one position to another.

Moreover, the observer may see several objects in diﬀerent directions from its current

position; the visible portions of these objects form the scene around the observer.

Constructing such a scene continuously is very natural for a human observer as the

human visual system can execute such tasks eﬀortlessly.

Suppose a robot wants to move from a starting position to a target position

without colliding with any object or obstacle around it. The robot constructs the

scene around itself from its current position and then guides its motion in the free

space lying between itself and the visible portion of the objects around it. The

positions of the robot and the objects can be represented in the computer of the

robot by their x, y and z co-ordinates and therefore, the scene consisting of visible

portions of these objects can be computed for the current position of the robot.

The problem of computing visible portions of given objects from a viewpoint has

been studied extensively in computer graphics [115]. Since the scene is constructed

from thousands of objects of diﬀerent shapes and sizes lying in diﬀerent positions, it

becomes a complex task from a computational point of view. Even computing visible

portions of one object in the presence of several other objects is a non-trivial task.

Moreover, computing such a scene for every position on the path of the robot is a

time-consuming task even for high-speed computers. Designing eﬃcient algorithms

for executing such movements of a robot in the presence of obstacles in a reasonable

period of time is one of the objectives in the ﬁeld of robot path planning [226].

2 Background

The above problem of robot path planning can be reduced to the corresponding

problem in two dimensions. If a mobile robot that maintains contact with the ﬂoor

is projected on the ﬂoor, the two-dimensional footprint of the robot can be modeled

as a polygon. Similar projections on the ﬂoor can now also be produced for all

obstacles. This process yields a map consisting of polygons in two dimensions. The

polygon corresponding to the robot can be navigated using this map by avoiding

collisions with polygonal obstacles. Thus a collision-free path of the robot can be

computed from its starting position to the target position. While navigating, the

visible portions of polygonal obstacles are computed to construct the scene around

the current position of the robot. Although such a representation in two dimensions

has reduced the complexity of the robot path planning problem, designing eﬃcient

algorithms for such computations remains a challenging task.

The notion of visibility has also been used extensively in the context of the art

gallery problem in computational geometry [271, 310, 333]. The art gallery problem

is to determine the number of guards that are suﬃcient to see every point in the

interior of an art gallery room. This means that every interior point of the room

must be visible to one of the guards so that all paintings in the gallery remain

guarded. There are many theorems and algorithms for the minimization of the

number of guards and their placement in the art gallery room.

The study of visibility started way back in 1913 when Brunn [67] proved a

theorem regarding the kernel of a set. Today visibility is used in many ﬁelds of

computer science including robotics [66, 226, 249, 283], computer vision [139, 168]

and computer graphics [93, 113, 115].

1.2 Polygon

A polygon P is deﬁned as a closed region R in the plane bounded by a ﬁnite set

of line segments (called edges of P ) such that there exists a path between any two

points of R which does not intersect any edge of P . Any endpoint of an edge of P is

called a vertex of P , which is a point in the plane. Since P is a closed and bounded

region, the boundary of P consists of cycles of edges of P , where two consecutive

edges in a cycle share a vertex. If the boundary of P consists of two or more cycles,

then P is called a polygon with holes (see Figure 1.1(a)). Otherwise, P is called a

simple polygon or a polygon without holes (see Figure 1.1(b)). The region R is called

the internal region or interior of P . Similarly, the regions of the plane excluding all

points of R are called the external regions or exterior of P . A vertex of P is called

convex if the interior angle at the vertex formed by two edges of that vertex is at

most π; otherwise it is called reﬂex. Note that the interior angle at a vertex always

faces the interior of P .

As deﬁned above, a simple polygon P is a region of the plane bounded by a cycle

of edges such that any pair of non-consecutive edges do not intersect. In this book,

1.2 Polygon 3

Figure 1.1 (a) In this polygon with holes, b and c are visible from a but not d. (b) In this

simple polygon (or a polygon without holes), b and c are visible from a, but not d.

we assume that P is given as a doubly linked list of vertices. Each vertex has two

ﬁelds containing x and y co-ordinates of the vertex and it has two pointers pointing

to the next clockwise and counterclockwise vertices of P . It can be seen that if edges

of P are traversed in counterclockwise (or clockwise) order, then the interior of P

always lies to the left (respectively, right) of the edges of P .

Let c

, c

, . . . , c

be the cycles on the boundary of a polygon P with h holes,

where c

represents the outer boundary of P . Let R

denote the region of the plane

enclosed by c

for all j ≤ h (see Figure 1.1(a)). Since P is a closed and bounded

region, R

⊂ R

for all j > 0. Moreover, R

∩ R

= ∅ where k 6= j and k > 0.

Therefore, R = R

− (R

∪ R

∪ . . . ∪ R

). Observe that if P is a simple polygon,

then R = R

as the boundary of P consists of only one cycle c

(see Figure 1.1(b)).

In this book, we assume that a polygon P with h holes is given in the form of h

cycles, where vertices of each cycle are stored in a doubly linked list as stated above

and there is an additional pointer to one vertex of each cycle of P to access that

cycle.

Two points p and q in P are said to be visible if the line segment joining p and q

contains no point on the exterior of P . This means that the segment pq lies totally

inside P. This deﬁnition allows the segment pq to pass through a reﬂex vertex or

graze along a polygonal edge. We also say that p sees q if p and q are visible in P .

It is obvious that if p sees q, q also sees p. So, we sometime say that p and q are

mutually visible. In Figure 1.1, the point a sees two points b and c, but not the

point d.

Exercise 1.2.1 Given two points p and q inside a polygon P , design a

method to determine whether p and q are visible in P .

Suppose a set of line segments in the plane is given such that they do not form

a polygon. Let A denote the arrangement of these line segments in the plane (see

4 Background

Figure 1.2 (a) In this arrangement of line segments A, points b and c are visible from a but

not d. (b) A convex polygon P where any two points are mutually visible. (c) A star-shaped

polygon P where the entire polygon is visible from any point of the kernel K.

Figure 1.2(a)). Two points p and q in the plane are said to be visible in the presence

of A if the line segment joining p and q does not cross any line segment in A. This

deﬁnition permits the segment pq to touch a line segment of A. In Figure 1.2, a

point a sees two points b and c, but not the point d.

Using the deﬁnition of visibility in a polygon, we deﬁne two special classes of

simple polygons called convex and star-shaped polygons. A simple polygon P is

called convex if every pair of points in P is mutually visible [176] (see Figure 1.2(b)).

It can be seen that the internal angle at every vertex of a convex polygon is at most

π [327]. A convex polygon can also be deﬁned as intersections of closed half-planes

which is bounded. A simple polygon P is said to be star-shaped if there exists a

point z inside P such that all points of P are visible from z (see Figure 1.2(c)). The

set of all such points z of P is called the kernel of P . The kernel of P is always

convex [67]. If P is a star-shaped polygon with respect to a point z, it can be seen

that the order of vertices on the boundary of P is same as the angular order of

vertices around z. We refer to this property by saying that the vertices of P are in

sorted angular order around z. It follows from the theorem of Krasnosel’skii [223]

that a simple polygon P is star-shaped if and only if every triple of convex vertices is

visible from some point of P [334]. Note that a convex polygon is also a star-shaped

polygon and all points of the convex polygon belong to the kernel.

Exercise 1.2.2 Prove that a polygon P is star-shaped if and only if every

triple of convex vertices is visible from some point of P [223].

Exercise 1.2.3 Prove that the kernel of a star-shaped polygon is convex.

剩余333页未读，继续阅读

身份认证购VIP最低享 7 折!

30元优惠券

musicbug

粉丝: 5

二维空间中的可视性算法概览

"高效剔除场景元素：可见序列集计算与应用（HELSINKI UT演示）

"云时代数据中心SDN网络解决方案学习教案PPT汇总

【技术创新】宽光谱带及多功能成像传感器助力汽车安全行驶（英文）

Visibility Comparisons over the Horizontal Path by Lidar and Visibility Meter

Modeling Mutual Visibility Relationship in Pedestrian Detection

Visibility_in_Bad_Weather_from_A_Single_Image

Managing visibility in Flutter – Flutter – Medium

Security Analytics – The Rising Need for Total Visibility

VIsibility属性

visibility

最新资源