博弈论与信息经济学：非合作博弈解析

"该资源为博弈论与信息经济学的非合作博弈理论篇章，涵盖了策略型博弈、扩展型博弈、贝叶斯博弈和动态贝叶斯博弈的主要内容，深入讲解了博弈的基本概念和理论。" 博弈论是研究决策者之间相互作用的数学工具，尤其在经济、政治和生物学等领域有广泛应用。非合作博弈理论是博弈论的一个分支，主要关注参与者不通过正式协议进行合作的情况。 在非合作博弈中，策略型博弈是最基础的形式。它涉及到两个或多个局中人，每个局中人都有自己的策略集，并且所有局中人对所有策略及可能的结果都有完全信息。策略型博弈包括以下三个关键元素： 1. **局中人**：博弈中的决策主体，例如在“囚徒困境”中，局中人是两个囚犯。 2. **策略**：每个局中人可以选择的行动或决策，可以是纯策略（如坦白或不坦白）或混合策略（概率性的策略选择）。 3. **支付函数**：定义了局中人在不同策略组合下的收益或损失，通常用支付矩阵来表示，如“囚徒困境”和“石头、剪刀、布”的支付矩阵。 **有限博弈**是策略型博弈的一个子类，局中人数量有限，且每个人的选择也是有限的。而**零和博弈**中，一方的收益恰好等于另一方的损失，如“石头、剪刀、布”游戏。 **扩展型博弈**则适用于描述行动顺序和信息不对称的博弈，比如在博弈过程中，局中人可以依据之前的行为调整策略。扩展型表述通常包含博弈树，显示了行动顺序和信息集。 **贝叶斯博弈**是在部分信息条件下的博弈，局中人对其他人的类型或概率分布有所了解，但不一定知道具体类型。**动态贝叶斯博弈**进一步考虑了时间的推移和信息更新，玩家基于新的信息不断调整自己的信念和策略。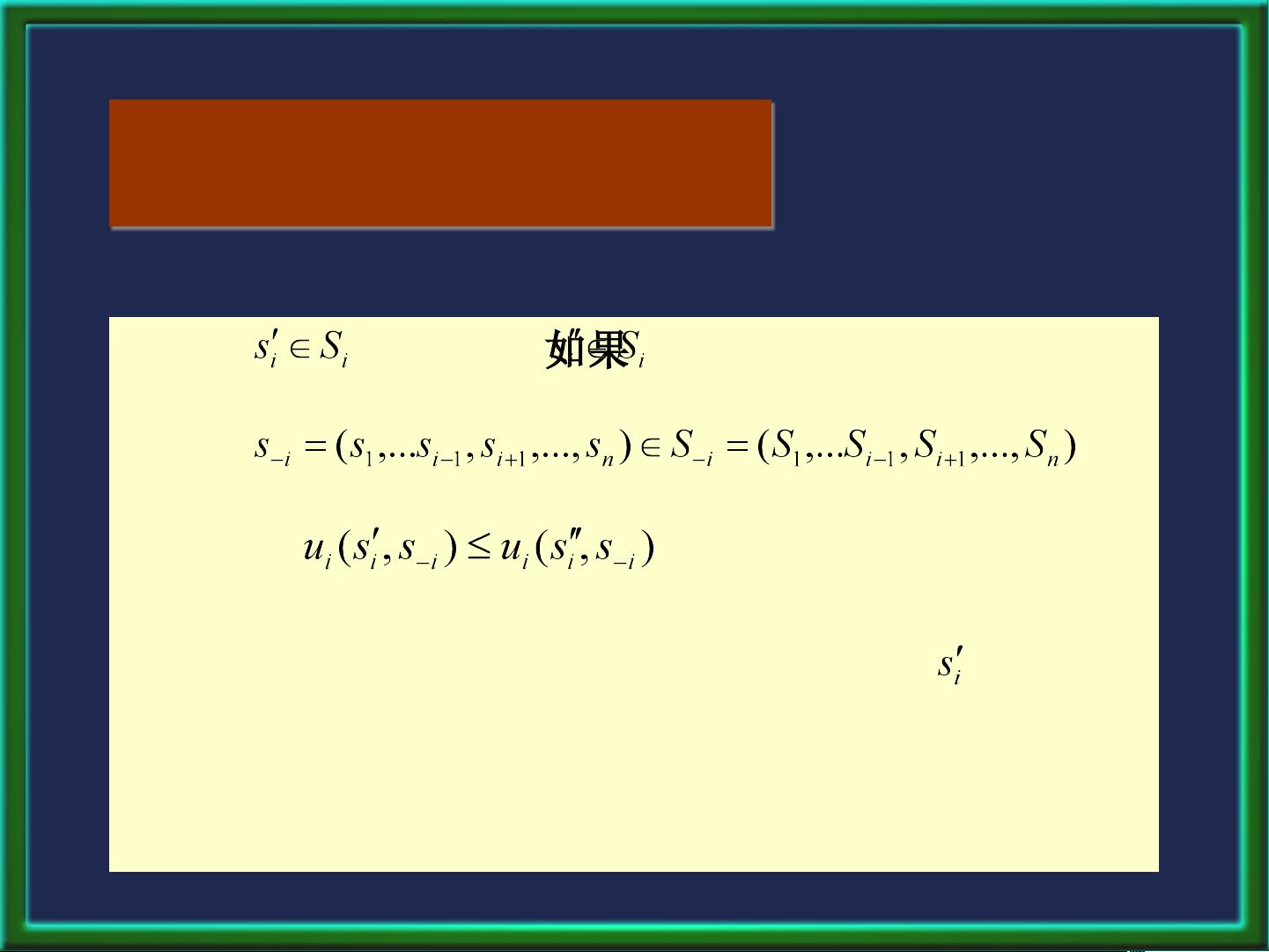 在策略型博弈中，**纳什均衡**是最核心的概念，它是所有局中人最优响应对方策略的状态，没有人有单方面改变策略的动机。**重复剔除严格劣策略**是一种寻找纳什均衡的方法，通过反复剔除对所有人来说都是严格劣势的策略，直到找到稳定状态。**混合策略纳什均衡**允许玩家随机化其策略，使得任何纯策略的期望支付都不优于其他玩家的期望支付。 博弈论与信息经济学的非合作博弈理论提供了一套理论框架，用于分析和理解在不合作情况下决策者之间的互动行为，这不仅有助于理解市场行为、政策制定，还可以应用于社会、军事和法律等诸多领域。