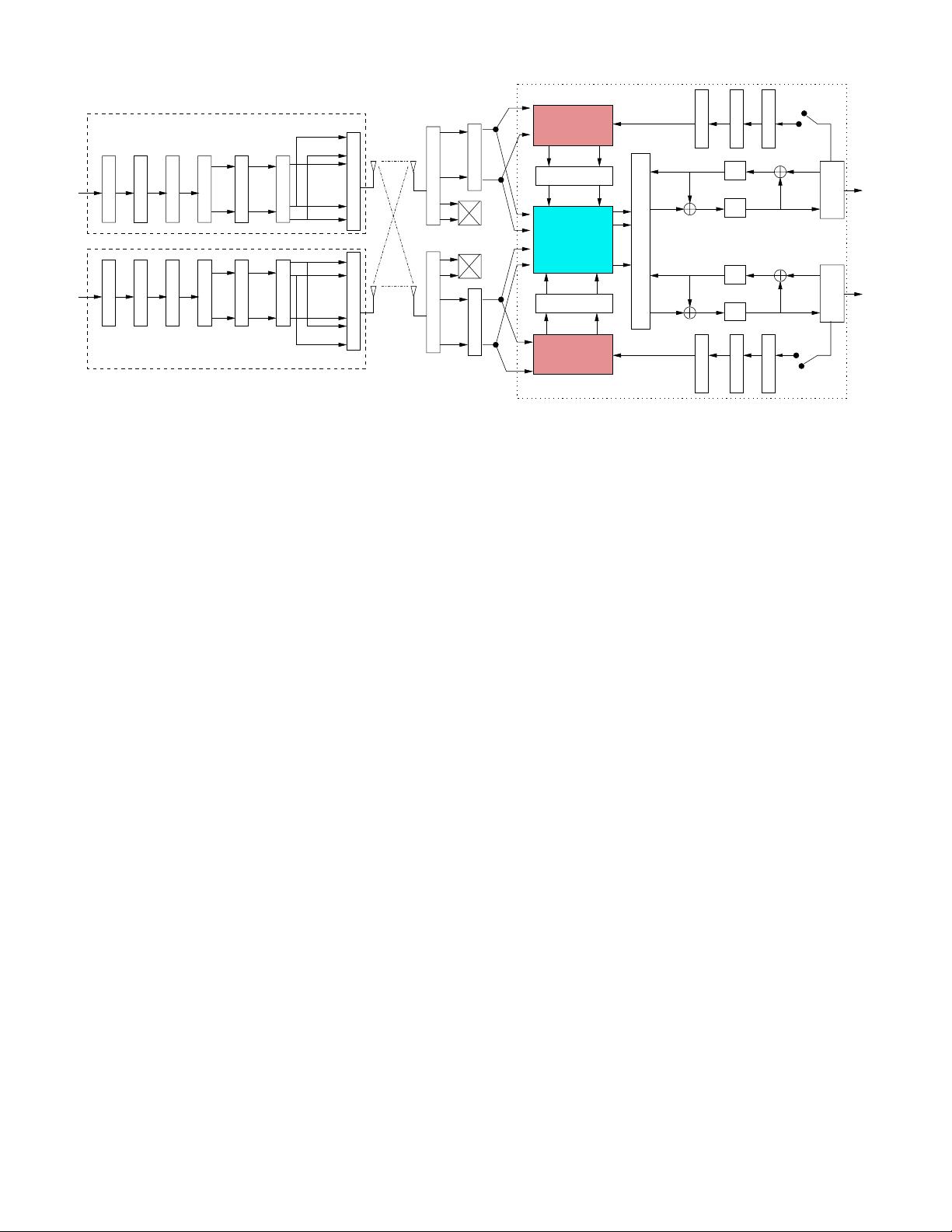
ZHANG et al. : TURBO MULTI-USER DETECTION FOR OFDM/SDMA SYSTEMS RELYING ON DIFFERENTIAL EVOLUTION AIDED ITERATIVE ... 1623
EncoderFEC
Modulator
1
U
1
Q
FEC
Parallel/Serial
Serial/ParallelSerial/Parallel
F F T F F T
F F T
F F T
CIR estimator
CIR estimator
Users’ data buffer & LLR calculator
EncoderFEC
Modulator
Parallel/Serial
I F F T
EncoderFEC
Serial/Parallel
Modulator
Pilot Allocation
Encoder
I F F T
Modulator
Serial/Parallel
Pilot Allocation
DE aided
(or DE aided
MSER−MUD)
aided ML−MUD
DE aided
Discrete DE
.
.
.
CP
decoder
SISO channel
Interleaver Π
decoder
SISO channel
CP{
.
.
.
.
.
.
.
.
.
y
1
[1]
y
1
[N]
y
Q
[1]
y
Q
[N]
.
.
.
CP
.
.
.
.
.
.
.
.
.
···
···
ˆ
h
1
1,1
ˆ
h
1
1,L
ˆ
h
Q
1,1
ˆ
H
Q
1,K
ˆ
H
Q
1,1
ˆ
H
1
1,1
.
.
.
···
···
ˆ
H
1
1,K
L
c,pr,b
U
L
c,e,b
U
Π
L
m,e,b
U
L
m,po,b
U
Π
−1
L
c,po,b
U
L
m,pr,b
U
ˆ
h
Q
1,L
b
U
Interleaver Π
.
.
.
b
1
L
c,pr,b
1
L
c,e,b
1
Π
L
m,e,b
1
L
m,po,b
1
Π
−1
L
c,po,b
1
L
m,pr,b
1
b
1
I
˜
X
1
X
1
[1]
X
1
[K]
.
.
.
˜
X
1
[1]
˜
X
1
[K]
.
.
.
b
1
C
b
1
.
.
.
.
.
.
Interleaver Π
˜
X
1
˜
X
U
.
.
.
x
1
[K − K
cp
]
CP{
x
1
[K]
x
1
[K]
.
.
.
.
.
.
x
1
[K − K
cp
]
b
U
I
˜
X
U
X
U
[K]
.
.
.
b
U
C
˜
X
U
[K]
.
.
.
Interleaver Π
b
U
MS-1
MS-U
˜
X
U
[1] X
U
[1]
x
U
[K]
x
U
[K − K
cp
]
x
1
[1]
.
.
.
.
.
.
x
U
[1]
.
.
.
x
U
[K]
x
U
[K − K
cp
]
Fig. 1. Uplink system model for Multi-user MIMO OFDM/SDMA. The subscripts m and c of L are associated with the MUD and channel decoder,
respectively, while the subscripts pr, po and e are used for representing the a priori, a posteriori and extrinsic information. The loop index of the superscript
(loop)
is omitted in this figure for avoiding confusion.
III. OPTIMIZATION PROBLEMS IN CHANNEL ESTIMATION
AND
MUD
In the context of the joint CE and MUD of the
OFDM/SDMA systems, the optimization problems can be
based on the log-likelihood function (LLF) conditioned both
on the CIR matrix h[s]=
h
1
[s] h
2
[s] ···h
Q
[s]
containing
all the CIR coefficients and on the users’ transmitted data
matrix X[s]=
X
1
[s] X
2
[s] ···X
U
[s]
T
∈ C
UK×K
,which
is given by
J(h[s], X[s]) =
Q
q=1
Y
q
[s] − X
T
[s]Fh
q
[s]
2
, (3)
where the received data obeys Y
q
[s] ∈ C
K×1
,the
FFT matrix F ∈ C
UK×UL
, the CIRs are given by
h
q
[s] ∈ C
UL×1
for q =1, 2, ···,Q,andL is the num-
ber of CIR taps, while the FD-CHTF vector Fh
q
[s]=
H
1
q
[s]
T
H
2
q
[s]
T
···
H
U
q
[s]
T
T
∈ C
UK×1
.
The joint ML optimization defined in Equation (3) may
become computationally prohibitive. The complexity of this
optimization process may be reduced to a tractable level by
invoking an iterative search loop that first explores the entire
set of possible channels h[s] and then searches the set of all
the possible transmitted data X[s], which is formulated as:
(
ˆ
h[s],
ˆ
X[s]) = arg min
X[s]
min
h[s]
J
h[s], X[s]
. (4)
A. Channel Estimation
In multi-user OFDM/SDMA systems, the CIRs can be
estimated using pilot symbols known at both the MSs and
the BS. For the block-fading scenario, the pilot symbols may
be assigned to the first OFDM symbol, which is also referred
to as a preamble. When the channel statistics are unknown,
the CIR estimate can be determined by minimizing the ML
cost function (CF). More specifically, the ML estimation of
the channel parameters is the solution of the following CF
minimization
ˆ
h
q
=argmin
h
q
J(h
q
)
=argmin
h
q
Y
q
[1] − X
T
[1]Fh
q
[1]
2
, (5)
where Y
q
[1] ∈ C
K×1
is the first received OFDM symbol,
while the transmitted data matrix X[1] ∈ C
UK×K
represents
the first transmitted OFDM symbols (pilot symbols) of the U
simultaneous users.
The standard least squares (LS) channel estimator (CE)
provides the solution of (5), which however is computationally
very expensive as it requires the inverses of the Q very-large
(U ·L) ×(U ·L) correlation matrices in order to obtain
ˆ
h
q
for
1 ≤ q ≤ Q. We propose an alternative DE aided CE to obtain
the solution of (5), which does not require the inverse of large-
dimensional matrices and is applicable in both training-based
and decision-directed channel estimations.
B. The ML-MUD Scheme
As a benefit of the CP, the OFDM/SDMA symbols do not
overlap and hence SDMA MUD processing can be applied
on a per-carrier basis [1, 3]. Upon invoking vector notations,
the set of equations constituted by Equation (1) for q =
1, 2, ···,Q at the k-th subcarrier of the s-th OFDM symbol
can be rewritten as:
Y[s, k]=H[s, k]X[s, k]+n[s, k], (6)
where Y[s, k] ∈ C
Q×1
, H[s, k] ∈ C
Q×U
, X[s, k] ∈ C
U×1
and n[s, k] ∈ C
Q×1
represent the received signals, the FD
MIMO channel matrix, the transmitted signals and the AWGN
noise, respectively. For notational convenience, the indices
[s, k] are omitted during our forthcoming discourse.
Briefly, the task of the MUD is to recover the transmitted
signals X ∈ C
U×1
of the U users from the received signals
given in Equation (6). Each element of X,sayX
u
, belongs

















