有向无环图(DAG)拓扑排序详细解析与C++实现

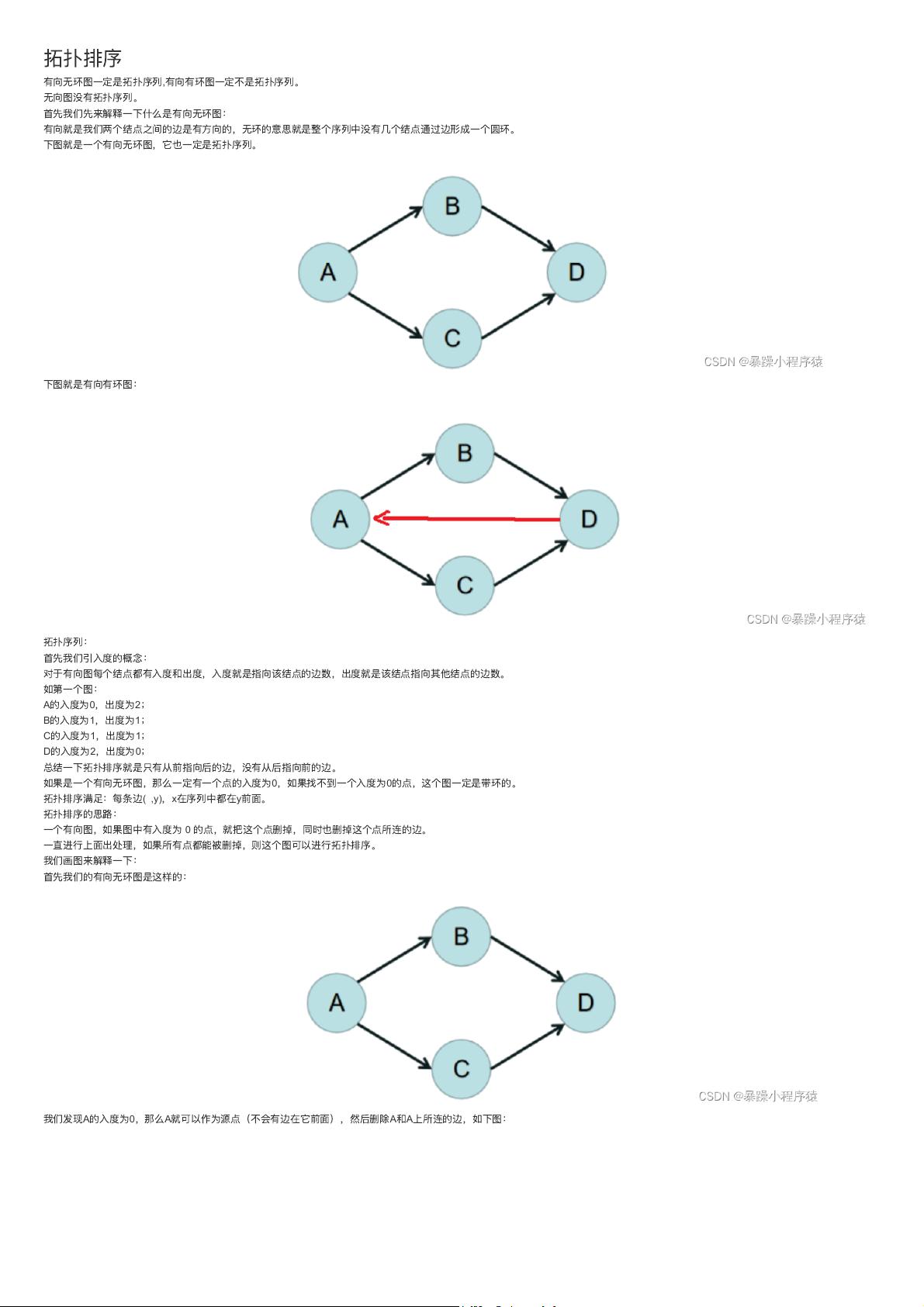
本文将详细介绍拓扑排序的概念、性质以及C++实现拓扑排序的算法。 拓扑排序是一种对有向无环图（Directed Acyclic Graph, DAG）进行排序的方法，它将图中的节点按照没有前驱（即入度为0）到有前驱的顺序排列。这种排序的结果是一个线性的序列，其中对于任何一条边 (u, v)，节点 u 总是出现在节点 v 之前。需要注意的是，有向有环图无法进行拓扑排序，而无向图由于其边的双向性，也没有拓扑序列的概念。 在有向无环图中，拓扑排序可以通过以下步骤进行： 1. 计算每个节点的入度，即指向该节点的边的数量。 2. 将所有入度为0的节点放入队列。 3. 当队列非空时，取出队首节点，并将其输出。然后找到与该节点相连的所有边，将对应的目标节点的入度减1。如果目标节点的入度变为0，将其加入队列。 4. 重复步骤3，直到队列为空或无法再将新的节点加入队列。如果队列为空，说明可以进行拓扑排序，输出的序列即为一种拓扑排序结果；否则，说明图中存在环，无法进行拓扑排序。 C++ 实现拓扑排序的代码通常包括一个辅助队列，用于存储入度为0的节点，以及一个邻接表表示图的结构。以下是一个简单的拓扑排序模板： ```cpp #include <queue> using namespace std; const int MAXN = 1005; // 图中最大节点数 int n, m; // n 为节点数，m 为边数 int d[MAXN]; // 存储每个节点的入度 int h[MAXN], ne[MAXN * MAXN], e[MAXN * MAXN]; // 邻接表表示图 bool topSort() { queue<int> q; for (int i = 1; i <= n; i++) { if (!d[i]) q.push(i); } int hh = 0, tt = -1; while (hh <= tt) { int t = q.front(); q.pop(); hh++; for (int i = h[t]; i != -1; i = ne[i]) { int j = e[i]; if (--d[j] == 0) q.push(j); } } return hh <= tt; // 如果所有点都入队了，返回true，表示存在拓扑序列 } // 其他用于构建图的函数... ``` 这个模板中，`h[]` 和 `ne[]` 是邻接链表的头部和下一个节点索引，`e[]` 是实际的节点连接。`topSort()` 函数首先初始化队列，然后在循环中不断处理队列中的节点，减少目标节点的入度并尝试将其加入队列，直到队列为空或无法继续。 总结来说，拓扑排序是一种有效的工具，常用于解决依赖关系的排序问题，例如任务调度、编译器中的语句排序等。在C++中，通过邻接表和队列数据结构可以高效地实现拓扑排序算法，其时间复杂度为O(n + m)，其中n是节点数，m是边数。