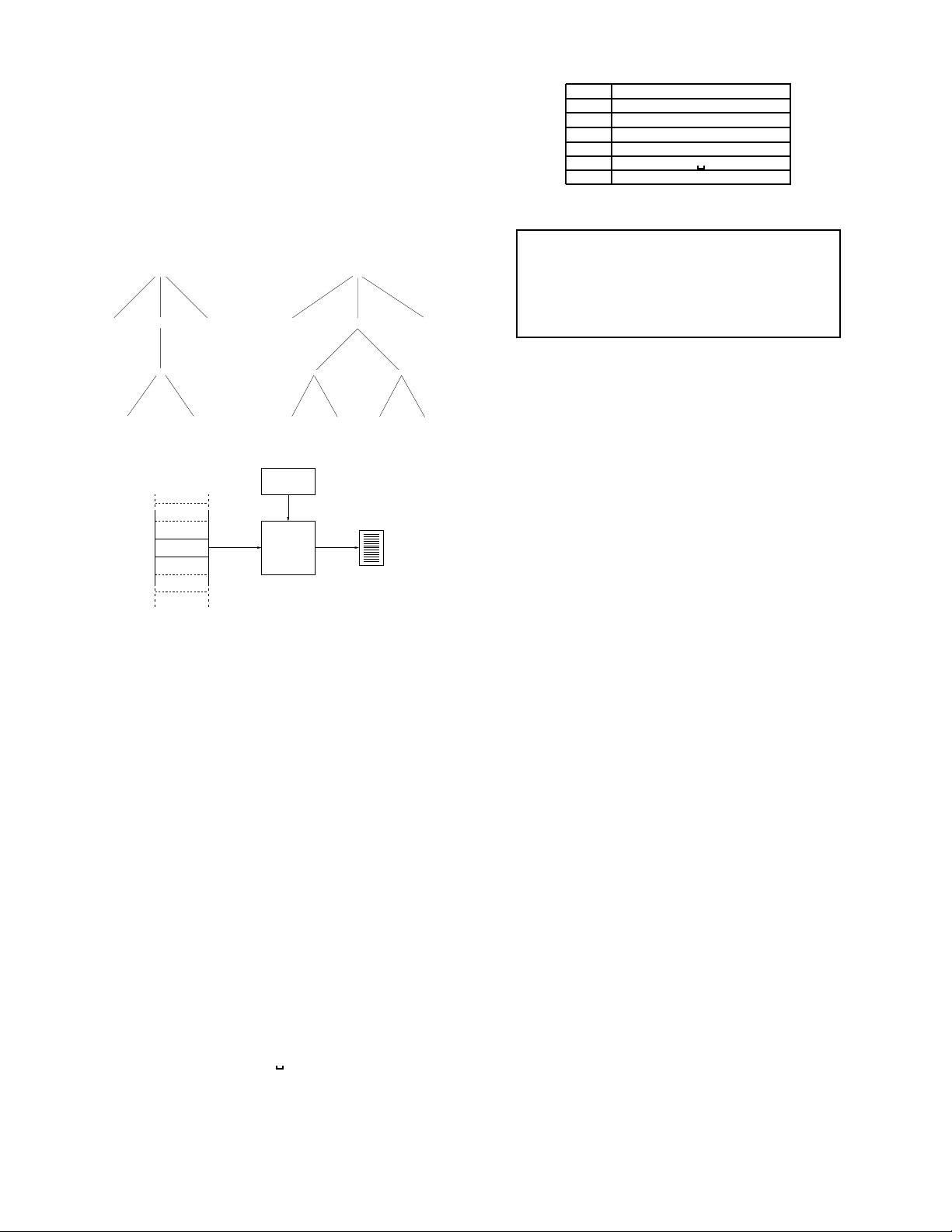
Schemas and values can be equivalently viewed as trees. Fig-
ure 3 shows the tree representation of schema S
1
and value x
1
.
A sub-tree of a schema tree is also a schema, and is called a sub-
schema of the original schema. A sub-value of a value is similarly
defined.
2.2 Model of Page Creation
We now describe a model for page creation. According to our
model (Figure 4), a value x (taken from a database shown on the
left) is encoded into a page using a template T . We denote the page
resulting from encoding of x using T by λ(T,x).
{ }
< >
B
{ }
s1
s
< > < >
τ
τ
τ
1
2
3
Figure 3: Example Schema and Instance
λ
(
T,x
)
(
T
)
x
Template
Output Pag
Figure 4: Model for Page Creation
Definition 2.1. (Template) A template T for a schema S, is de-
fined as a function that maps each type constructor τ of S into an
ordered set of strings T (τ ), such that,
1. If τ is a tuple constructor of order n, T (τ ) is an ordered set
of n +1strings C
τ 1
,...,C
τ (n+1)
.
2. If τ is a set constructor, T (τ ) is a string S
τ
(trivially an or-
dered set of unit size). 2
Optionally, we represent template T as T
S
to denote that T is
defined for schema S. For case 1 (resp. case 2) of Definition 2.1,
we say string C
τi
(1 ≤ i ≤ n +1)(resp. string S
τ
)isassociated
with type constructor τ. If a string is associated with a type con-
structor in a template, any token that occurs within the string is also
said to be associated with the type constructor.
Example 2.2. A template T
1
S
1
for Schema S
1
of Example 2.1
is given by the mapping, T
1
(τ
1
)=A, B, C, D, T
1
(τ
2
)=H,
T
1
(τ
3
)=E,F, G (each letter A − H is a string). Template
T
1
S
1
tells us how to encode a page from a value. For example, the
encoding λ(T
1
,x
1
) is the string AtBEf
1
Fl
1
GHEf
2
Fl
2
GCcD.
For concreteness, let strings (A − H) be as shown in Figure 5(a)
( represents an empty string and
represents white space ). The
web page corresponding to the book tuple C Programming Lan-
guage, {Brian, Kernighan, Dennis,Ritchie }, $30.00 is
shown in Figure 6(b). 2
A htmlbodybBook :/b
B by
C bCost :/b
D /body/html
E,G
F
H and
Figure 5: Template of Example 2.2
html
body
bBook :/bC Programming Language
by Brian Kernighan and Dennis Ritchie
bCost :/b$30.00
/body
/html
Figure 6: Template and Page of Example 2.2
Formally, given a template, T
S
, the encoding λ(T,x) of an in-
stance x of S is defined recursively in terms of encoding of sub-
values of x. Since it causes no ambiguity, we use the λ(T,x) nota-
tion for values x that are instances of sub-schema of S.
1. If x is of basic type, B, λ(T,x) is defined to be x itself.
2. If x is a tuple of form x
1
,...,x
n
τ
t
, λ(T,x) is the string
C
1
λ(T,x
1
) C
2
λ(T,x
2
) ...λ(T,x
n
) C
n+1
. Here, x is an
instance of sub-schema that is rooted at type constructor τ
t
in S, and T (τ
t
)=C
1
,...,C
n+1
.
3. If x is a set of the form {e
1
,...,e
m
}
τ
s
, λ(T,x) is given by
the string λ(T,e
1
) Sλ(T,e
2
) S ... S λ(T,e
m
). Here x is
an instance of sub-schema that is rooted at type constructor
τ
s
in S, and T (τ
s
)=S.
We represent a template using an infix notation. For example,
the template of Example 2.2 is represented as A ∗ B{E ∗ F ∗
G}
H
C ∗ D. The “∗” symbol is similar to UNIX wild-card, and
indicates positions where values of basic type appear in an encod-
ing using the template. Note that string H, associated with τ
2
of
Example 2.2 is placed as subscript of {}.
Our model captures the requirement that the web pages be gen-
erated in a consistent manner. In particular, it ensures that values
for the same attribute in a tuple occur in the same relative position
with respect to the values of other attributes, in all the pages. In
Example 2.2 above, the book name always occurs before the list of
authors and the price. The encoding of the set captures the intuition
that elements of a set are usually listed contiguously, and that the
elements of the set are formatted in a similar manner.
2.3 Optionals and Disjunctions
As we saw in Section 2.1, a schema is built from two kinds of
type constructors, tuple and set, and the basic type B. There are two
other kinds of type constructors that occur commonly in the schema
of web pages, namely, optionals and disjunctions. For example the
list-price of a book in Amazon book pages is optional since only
pages for books sold at a discount price have list-price information.
As an example of a disjunction, an address information in a web
page could be in one of two formats, based on whether the address
is a US address or not, in which case the schema of the address is
a disjunction of the schema for US addresses and the schema for
non-US addresses.
We view optionals and disjunctions as special type constructors
built from set and tuple constructors. If T is a type, then (T )?
represents the optional type T , and is equivalent to {T }
τ
with the









