C语言实现后缀表达式求解的详细代码解析

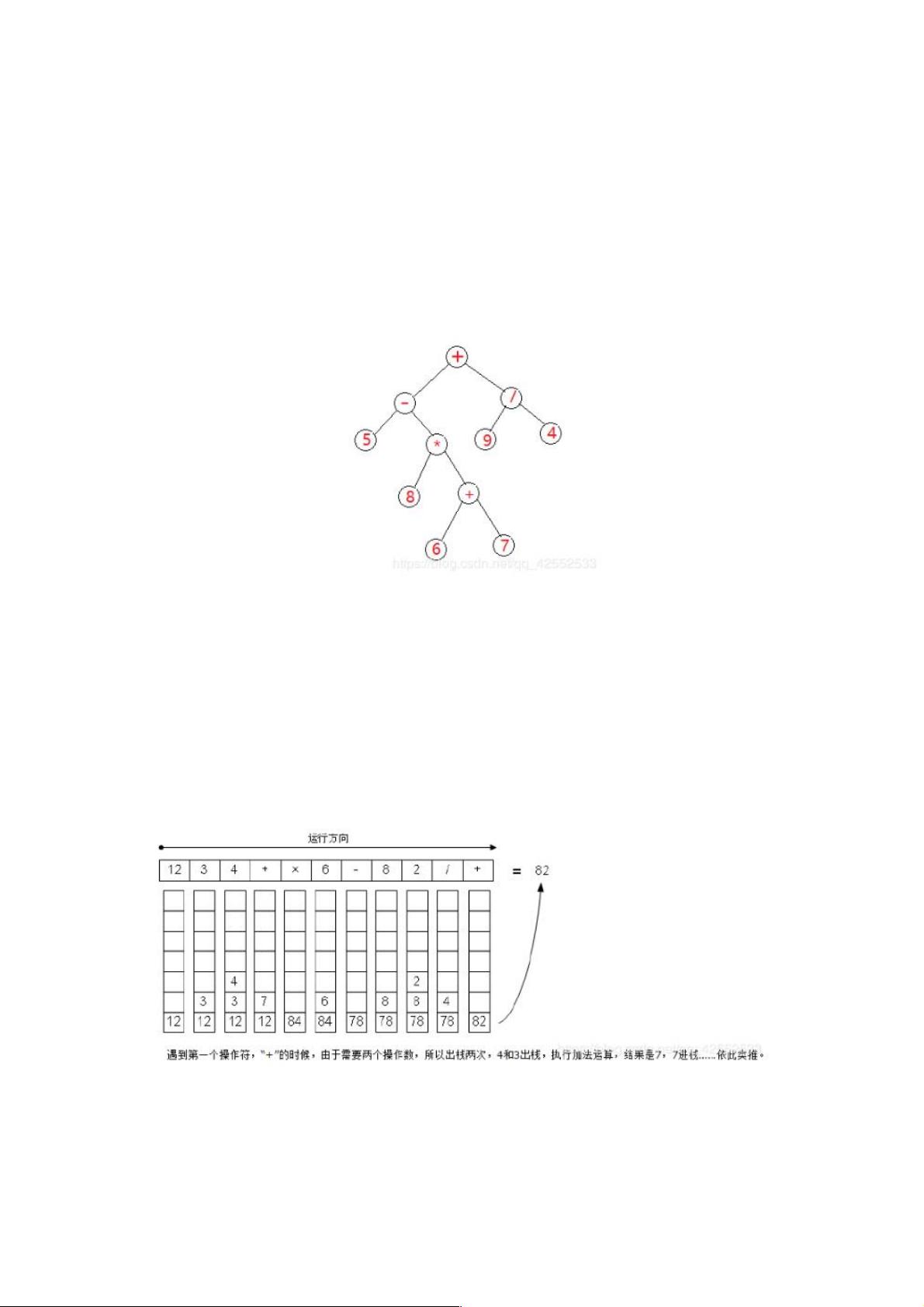
"C语言利用栈实现对后缀表达式的求解，主要涉及逆波兰表达式、中缀表达式到后缀表达式的转换以及逆波兰表达式的计算原理和算法实现。" 在计算机科学中，表达式的求解通常涉及到不同的表示方式，其中后缀表达式（也称为逆波兰表达式）是一种简化计算过程的有效方法。本文主要讨论如何用C语言通过栈的数据结构来处理后缀表达式的计算。 后缀表达式是基于中缀表达式（常规的算术运算符位于操作数之间）的一种表示形式。它的特点在于运算符放在操作数之后，使得无需括号就能清晰地确定运算顺序。例如，中缀表达式 "5-8*(6+7)+9/4" 可以转换为后缀表达式 "5867+*-94/+"，其中 "+"、"*"、"/" 分别对应加法、乘法和除法运算。 转换过程通常通过构建语法树并进行后序遍历完成。在这个例子中，我们首先遍历中缀表达式，构建对应的语法树，然后进行后序遍历，得到的序列即为后缀表达式。 逆波兰表达式的优势在于，它可以方便地使用栈进行计算。算法的基本思路如下： 1. 遍历后缀表达式的字符： - 当遇到数字或小数点时，收集这些字符直到遇到非数字字符，然后将其转换为浮点数并压栈。 - 当遇到运算符时，弹出栈顶的两个元素（假设为右操作数和左操作数），根据运算符执行相应的操作（如加、减、乘、除），并将结果压回栈中。 2. 当整个后缀表达式遍历完，栈顶的元素即为表达式的结果。 以下是一个简化的C语言实现片段，展示了如何处理后缀表达式的计算： ```c void CalFunction(SqStack *S, char str[]) { // 实现浮点型数据后缀表达式的加减乘除 Elemtypenumber, e, d; char arr[MAXBUFFER]; int i = 0, j = 0; InitStack(S); while (str[i] != '\0') { // 处理数字 while (isdigit(str[i]) || str[i] == '.') { // 收集数字字符 arr[j++] = str[i++]; arr[j] = '\0'; if (j >= MAXBUFFER) { printf("输入单个数据过大！\n"); return; } if (str[i] == '') { // 字符串结束或遇到非数字字符 number = atof(arr); // 将数字字符串转化为double型数据 PushStack(S, number); // 压栈 j = 0; // 重置j准备处理下一个数据 break; } } // 遇到运算符进行运算 switch (str[i]) { case '+': PopStack(S, &e); PopStack(S, &d); PushStack(S, d + e); break; case '-': PopStack(S, &e); PopStack(S, &d); PushStack(S, d - e); break; // ... } i++; } // 结果在栈顶 PopStack(S, &result); } ``` 这段代码定义了一个`CalFunction`函数，它接收一个字符串类型的后缀表达式和一个栈作为参数。在遍历字符串的过程中，它会根据遇到的字符执行相应的操作。最后，栈顶的元素就是计算结果。 C语言通过栈实现对后缀表达式的求解，不仅简化了表达式的解析，还使得计算过程更易于理解和实现。这种技术广泛应用于计算器程序、编译器和解释器的设计中。