主成分分析详解：多元统计解决实际问题关键步骤与应用实例

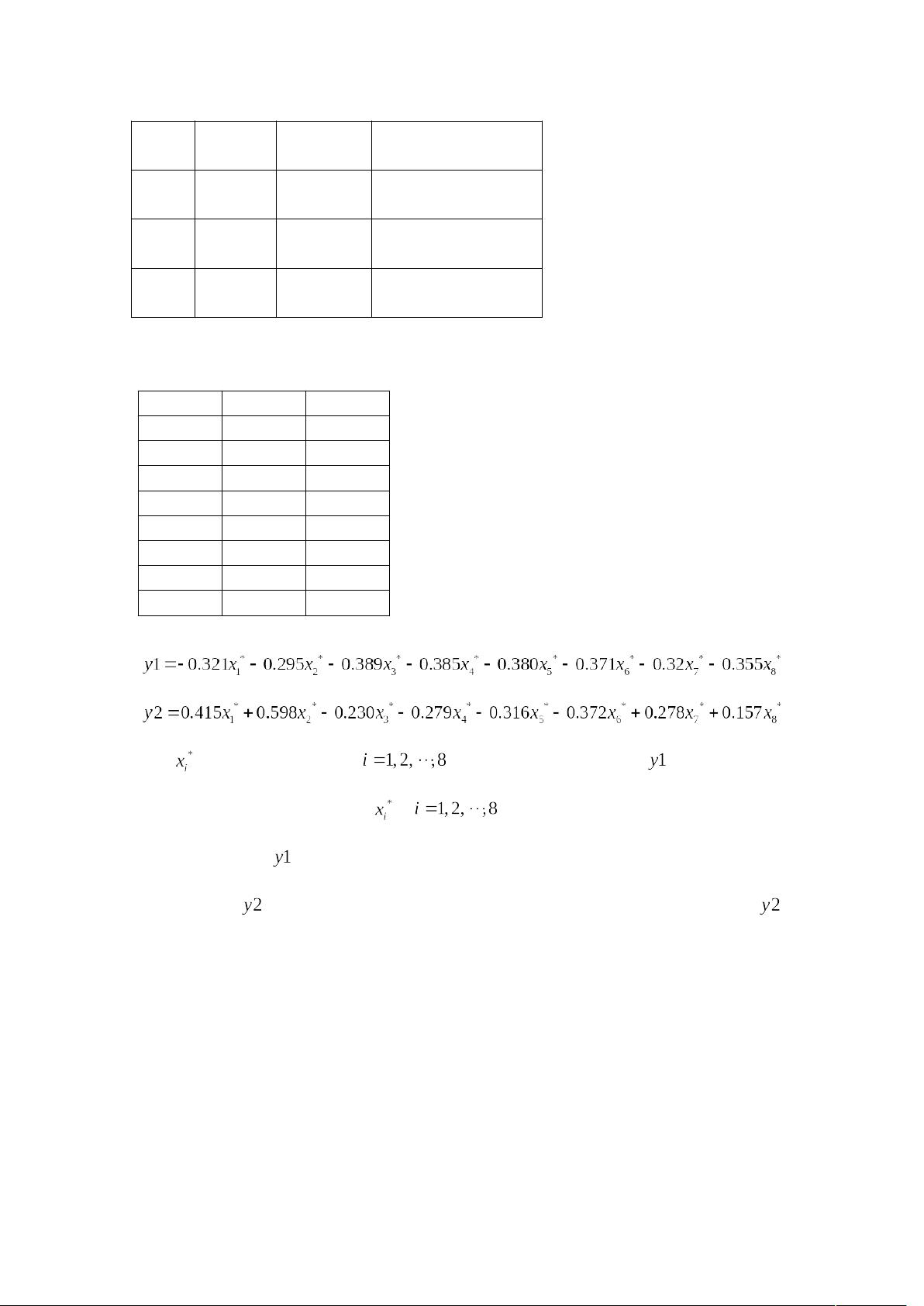
主成分分析是一种重要的多元统计分析方法，常用于降维和数据简化，尤其在处理大量复杂数据集时，有助于减少冗余信息并保持关键特征。该方法通过计算样本的协方差或相关矩阵，提取出数据的主要方向或因子，这些因子代表了原始变量的最大变异。 报告的核心内容包括以下几个方面： 1. 计算步骤： - 输入样本观测值，进行预处理，如计算每个指标的样本均值和标准差。 - 标准化数据，构建样本相关阵或协方差阵，确保分析的公平性。 - 求解相关矩阵或协方差矩阵的特征值和特征向量，得到正则化特征向量，即主成分的负载矩阵。 - 确定主成分数量，通常选择累积方差贡献率超过85%或80%的特征作为主要因子。 - 计算主成分的样本值，并用它们替换原始数据进行后续统计分析。 2. 例题一： - 通过对比协方差矩阵和相关矩阵的主成分分析，展示从不同矩阵出发可能得到不同的结果。例如，从协方差矩阵出发，第一主成分可能更侧重于方差较大的变量，这可能掩盖其他变量的影响。 3. 实际应用： - 主成分分析不仅用于理论研究，还能解决实际问题。通过主成分，可以发现数据中的潜在结构，例如在市场分析中识别消费者的消费模式，或者在金融领域中识别投资组合的风险和收益关联。 4. S型与R型区别： - R型主成分分析是基于标准化数据进行的，而S型则不进行标准化，适用于变量尺度不一致的情况。选择哪种方法取决于具体问题和数据特性。 主成分分析是一个强大的工具，它帮助我们理解和操纵数据的内在结构，减少数据维度，便于进一步的分析和可视化。通过学习和实践主成分分析，研究人员和分析师能够更有效地提取数据的关键信息，提升数据分析的效率和精度。