MATLAB实现FFT进行信号检测与谱分析
187 浏览量
更新于2024-08-04
收藏 411KB DOC 举报
"该文档是关于MATLAB实现离散傅里叶变换(DFT)和快速傅里叶变换(FFT)的实验报告,旨在通过实验掌握FFT函数的运用,进行信号检测与谱分析,并理解信号截取长度和采样频率对谱分析的影响。实验内容包括计算信号功率谱以及通过不同N值的FFT分析信号频谱。"
实验中涉及的知识点主要包括:
1. **离散傅里叶变换(DFT)**: DFT是一种数学工具,用于将离散时间信号转换到离散频率域,表达式为\( X[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi kn/N} \),其中\( X[k] \)是频率分量,\( x[n] \)是时间序列,\( N \)是序列长度。
2. **快速傅里叶变换(FFT)**: FFT是DFT的高效算法,MATLAB中的`fft`函数就是实现FFT的。它通过分解序列的长度来减少计算复杂度,使得计算速度大大提升。
3. **功率谱分析**: 功率谱是信号在频域内的能量分布,可以反映信号各频率成分的功率。在实验中,通过\( P = Y \cdot conj(Y) / N \)计算,其中\( Y \)是经过FFT处理后的复数序列,\( conj(Y) \)是其共轭,\( N \)是FFT点数。
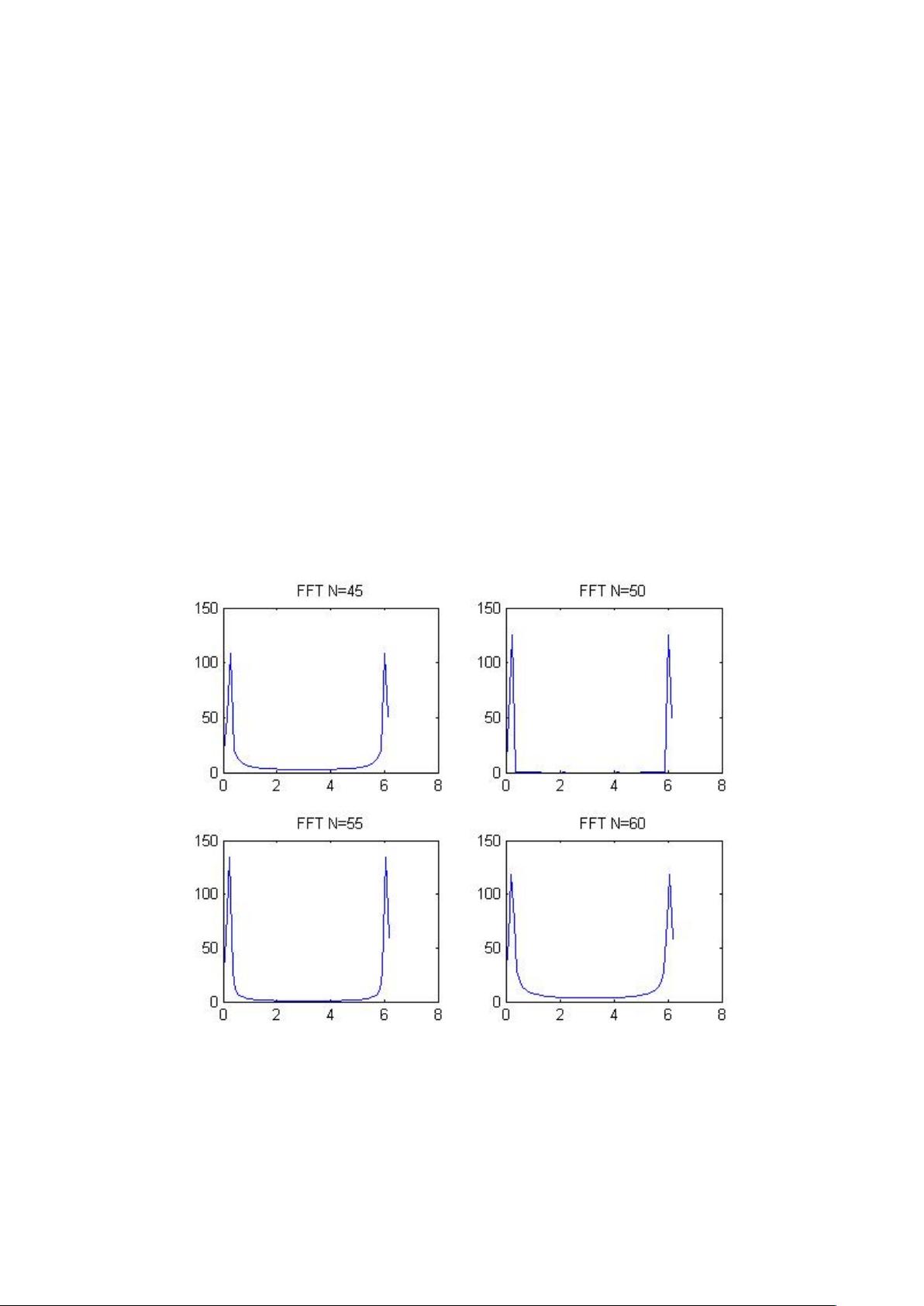
4. **信号截取长度的影响**: 截取长度决定了频谱分辨率,更长的截取长度意味着更高的频率分辨率,但会增加计算量。实验中通过改变FFT点数N,观察信号频谱的变化。
5. **采样频率的作用**: 采样频率决定了信号的最高可辨频率,根据奈奎斯特定理,采样频率应至少为信号最高频率的两倍。改变采样频率会改变频率轴上的间隔,影响频谱的显示。
6. **MATLAB编程实践**: 实验程序中使用了MATLAB的`fft`函数,`subplot`用于创建多子图,`plot`函数绘制频率与幅值的关系图,`abs`函数获取复数的绝对值,`conj`函数取复数共轭。
7. **频谱分析的应用**: 在信号检测中,通过观察频谱可以识别信号的成分,例如实验中的正弦波和余弦波。
8. **频率轴数字频率和实际频率的关系**: 数字频率是通过采样频率除以FFT点数得到的,实际频率是通过数字频率乘以采样率(采样频率的倒数)得到的。
通过这个实验,学生能够深入理解DFT和FFT的概念,掌握MATLAB在数字信号处理中的应用,并对信号检测、频谱分析及其影响因素有直观的认识。
2062 浏览量
16515 浏览量
2112 浏览量
7431 浏览量
1564 浏览量
766 浏览量
2165 浏览量
matlab大师
- 粉丝: 2863
最新资源
- ASP.NET实现上传视频自动抓取首帧图片功能
- PHP实现的单页商城源码—茅台酒专属定制
- 基于SpringMVC+Mybatis+EasyUI的完整后台管理系统开发教程
- fsconsul:实现Consul配置数据的文件系统写入
- C语言CS220课程项目:Spring21版本解读
- C语言实现队列练习:括号匹配检测算法
- VC代码美化工具——美化C++代码的自定义版式设计
- 免费下载个人收集的Timeline资源
- 掌握Excel导入导出:必备jar包解析
- Elasticsearch与EMQTTD集成开发插件
- 实现Excel到LaTeX转换的Javascript工具
- 全新Stereoscopic_Player_1.71 3D播放器注册版体验
- Android 4.4特性解析:实现透明状态栏的简易方法
- 新宁地方婚庆门户网源码发布与测试指南
- C#版固定资产管理系统源码支持SQL和Access数据库
- Spring Boot 应用开发实战:从零开始构建项目