C语言实现FFT程序：TMS320C64x处理器在LFM信号处理中的应用

"本文档主要讨论如何利用C语言实现快速傅里叶变换(FFT)算法，特别是针对大量数据的处理，并介绍了LFM信号实时脉冲压缩的实现以及TMS320C64x处理器在FFT计算中的应用。此外，还涉及到FFT中的蝶形算法及其编程方法，以及DFT的基本性质。" 在C语言中实现FFT，关键在于理解FFT的算法原理，其中最常用的是基2的FFT，即Cooley-Tukey算法，它通过将大问题分解为小问题来加速计算。在处理大量数据时，可以设计程序以动态调整数据点数，提高灵活性。首先，需要确定要处理的数据点数，然后根据数据点数构建相应的蝶形结构图。每个蝶形操作包括两个复数的乘法和一次加法，这两个复数分别对应于DFT的复指数项。 LFM（线性调频）信号的实时脉冲压缩通常需要FFT来实现频域脉压。TMS320C64x处理器因其高性能和高效的指令执行能力，成为实现这一任务的理想选择。该处理器具有8个功能单元，包括2个乘法器和6个算术单元，能够在单个时钟周期内执行多条指令，极大地提升了计算效率。此外，它的指令打包和条件执行特性进一步减少了代码长度和功耗，优化了分支执行性能。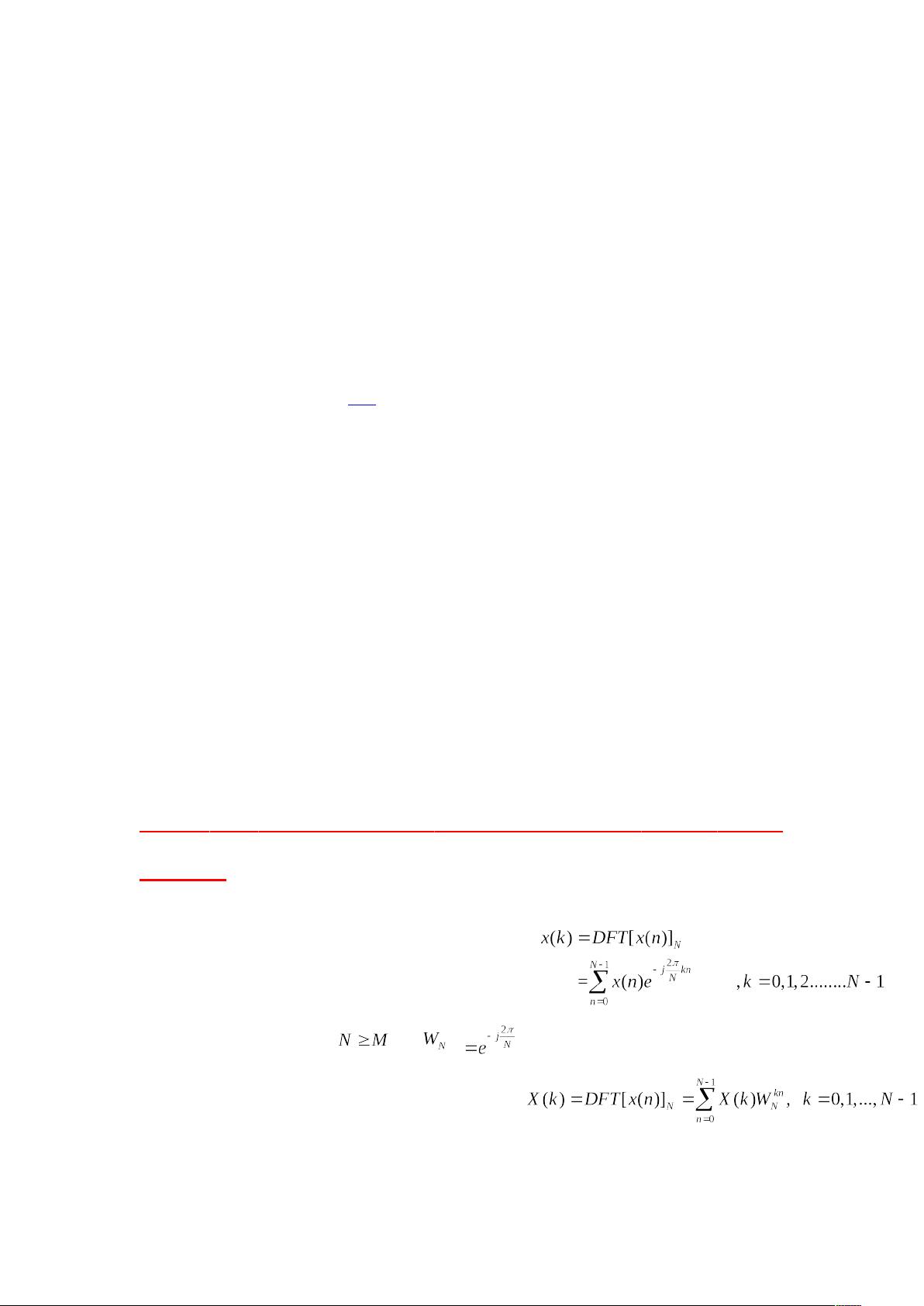 为了编写FFT程序，我们需要理解DFT的数学基础。对于长度为M的序列x(n)，N点DFT定义为一系列复数的乘积累加。DFT的重要性质包括线性和隐含周期性，这些性质对于理解和优化算法至关重要。线性性质表明DFT是对输入序列进行线性操作，而隐含周期性意味着DFT的结果具有周期性，这在处理循环卷积和相关问题时特别有用。 在编程实现时，我们需要将DFT的计算过程分解为多个阶段，每个阶段对应一组蝶形操作。通过递归地应用这个过程，可以从原始序列逐步计算出完整的DFT。为了提高效率，我们通常会采用位反转排序和分治策略，确保计算过程的对称性。 利用C语言实现FFT涉及深入理解数字信号处理理论，特别是DFT和FFT算法，以及熟悉高效的处理器架构，如TMS320C64x，来优化计算过程。在实际编程中，需要注意数据结构的设计、内存管理以及算法的优化，以确保在处理大量数据时能够高效运行。