计算机数值分析习题与答案解析

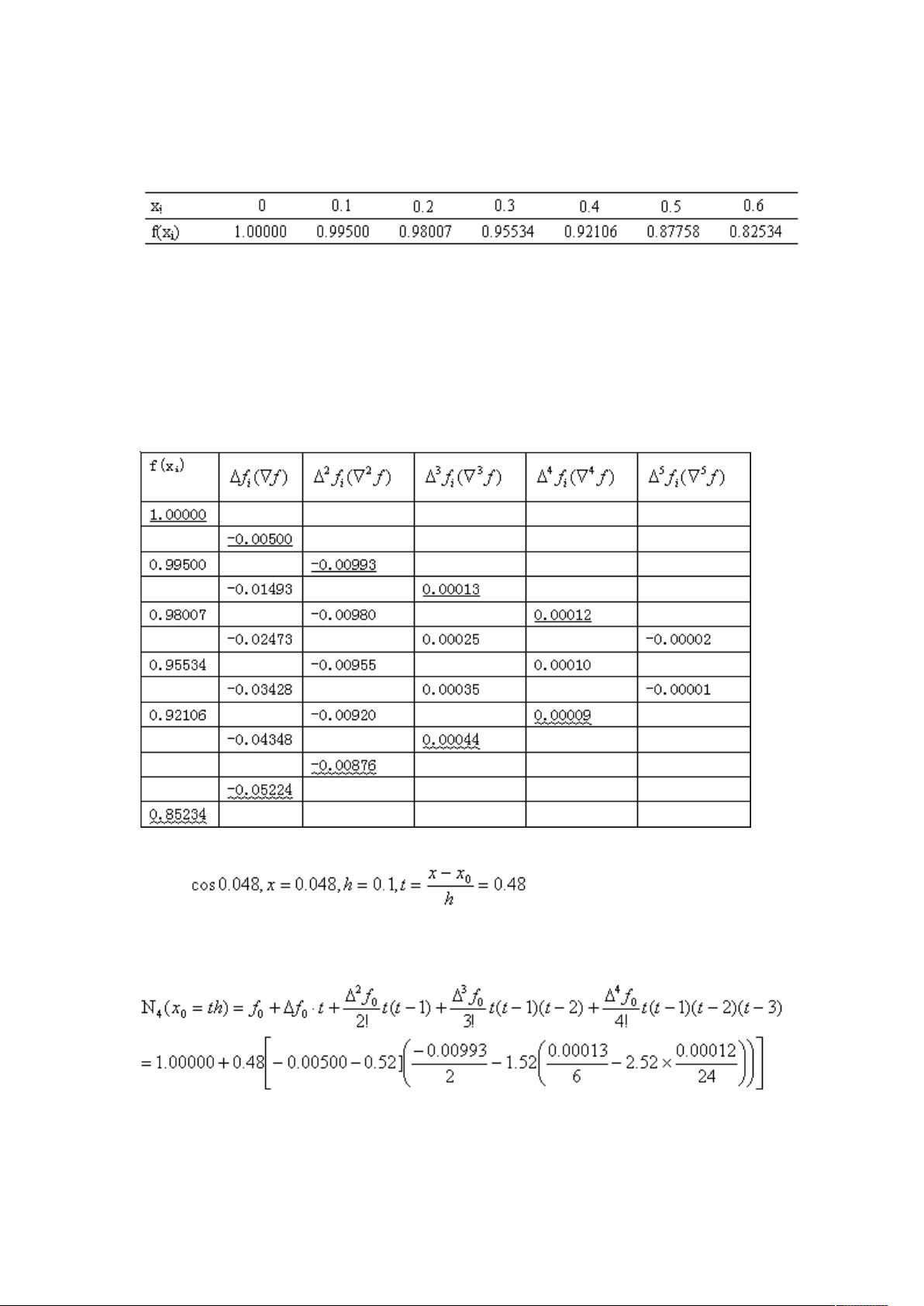
"该资源是关于计算机数值分析的习题集与解答，主要针对清华大学出版的第四版教材，提供课后习题的答案，旨在帮助学习者深入理解和掌握课程内容。内容涉及第一章绪论以及第二、三章插值与函数逼近的相关问题。" 详细知识点解析： 1. **数值分析基础**： - 绪论部分介绍了误差分析的基础知识，如相对误差、误差限的计算。例如，题目中提到的lnx的误差限可以通过公式(1.2.4)计算，通过相对误差δ求得绝对误差限。 - 有效数字的概念及其与误差限、相对误差限的关系被用来判断近似值的精度，如题目中的四舍五入得到的近似值。 2. **数值计算策略**： - 避免相近数相减以提高计算准确性，这是数值计算中减少误差的一种策略。例如，题目中给出了两个公式，通过变换形式来避免可能的计算误差。 3. **插值与函数逼近**： - 插值法是数值分析中的重要概念，如线性插值和二次插值。在习题中，使用Lagrange插值或Newton插值方法计算ln0.54的近似值，并通过误差估计公式(5.8)估算误差限。 - 函数表的步长选择影响插值法的精度，如在求解[pic]的近似值时，需要确保误差不超过特定值，这涉及到误差估计公式和步长h的计算。 - 均差与导数的关系在求导数值时有重要作用，如题目中通过[pic]关系求[pic]的值。 - 对于多项式插值，如题目中的[pic]，可以利用均差对称性来求解特定点的值。 4. **差分与函数关系**： - 差分是数值微分的一种方法，证明[pic]涉及直接展开差分定义，展示了差分与导数之间的联系。 5. **二次插值法的应用**： - 在插值问题中，二次插值法用于构建二次多项式近似函数，以逼近给定数据点的函数。在解决实际问题时，如要求误差不超过特定值，需要计算合适的步长h。 总结，这份资源涵盖了数值分析的基本概念，包括误差分析、插值法和函数逼近，适合学习者巩固理论知识并提升实际计算技能。通过解决这些习题，学习者能够深入理解数值计算的方法，并学会如何评估和控制计算误差。