大规模强化学习中的值函数近似法

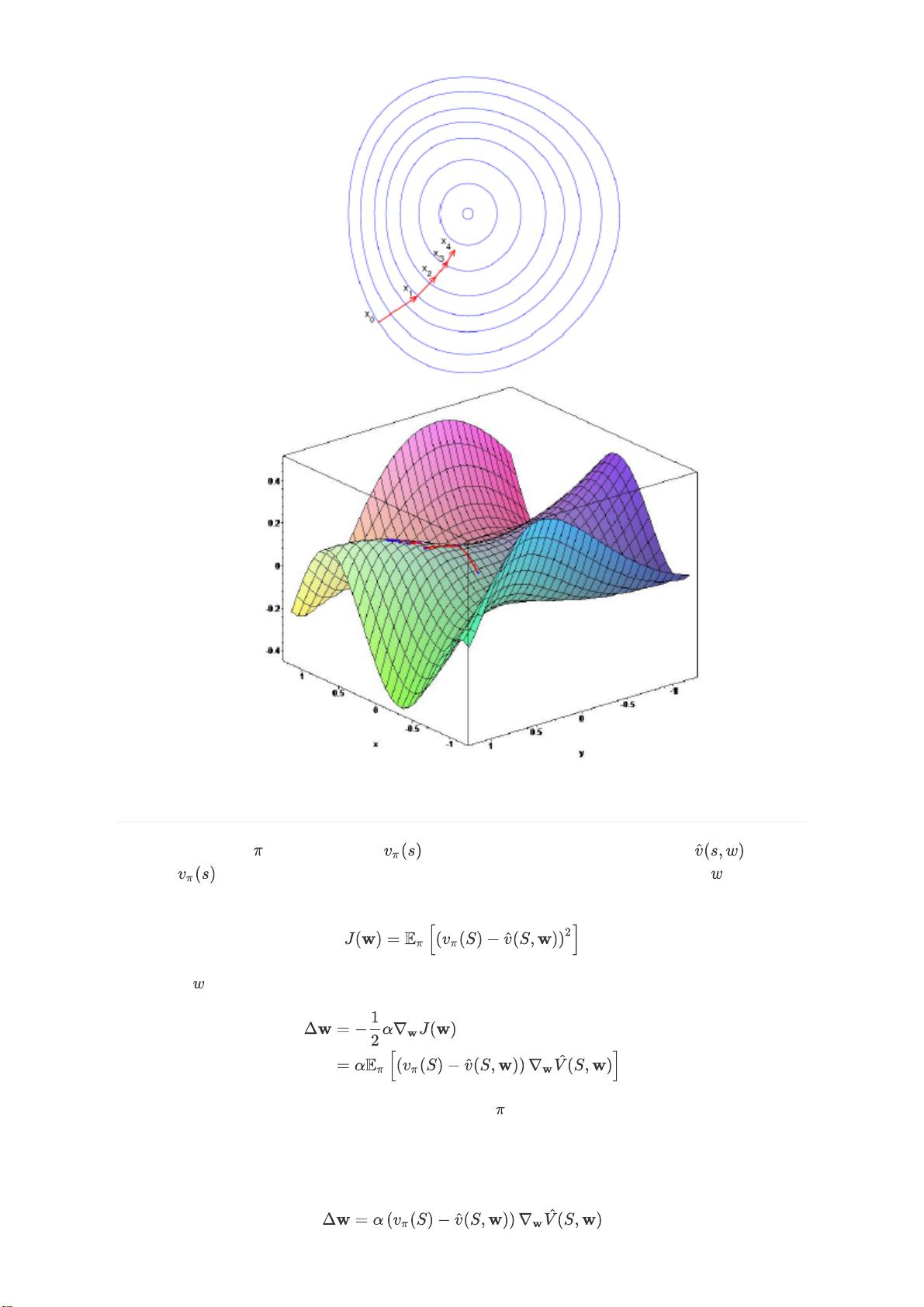
"值函数近似法在强化学习中扮演着重要的角色，特别是在处理大规模问题时。这种方法通过构建近似函数来代替传统的表格方法，解决了存储和计算效率的问题。" 值函数近似法主要应用于那些状态空间过于庞大的强化学习任务，如棋类游戏中的Backgammon和围棋，它们的状态数量巨大，无法用表格方式存储所有状态的价值。值函数近似法通过函数（如线性函数或神经网络）来近似状态值函数V(s)或动作值函数Q(s, a)，使得我们可以处理不可见甚至无穷状态的情况。 函数近似主要有三种模式： 1. 输入状态，输出状态值V(s)。 2. 输入状态和动作，输出动作值Q(s, a)。 3. 输入状态，输出所有可能动作的Q值。 选择的近似函数类型多样，包括线性函数、神经网络、决策树、最近邻算法等。在可微分的近似函数中，线性函数和神经网络是最常见的选择，因为它们能够适应强化学习环境中非静态和非独立同分布的数据特性。 优化过程中，常用的目标函数是均方误差(MSE)，用于衡量Q网络预测值与实际目标值的差距。优化算法常常采用梯度下降法，其中目标函数T关于参数θ的梯度表示了参数调整的方向。学习率α决定了每次参数更新的步长。随机梯度下降是梯度下降的一个变种，它在每次迭代时只使用一个样本的梯度信息，适合处理大规模数据集，尤其是在数据非独立同分布的情况下。 在实际操作中，强化学习算法会从经验池中抽取数据，根据固定的旧参数计算Q值，并利用这些数据更新Q网络的参数，以逐渐减小目标函数MSE，从而逐步优化Q函数的近似精度。这个过程可以是基于蒙特卡洛（MC）方法，也可以是基于时间差分（TD）学习，例如TD(λ)或Q-learning。 值函数近似法是强化学习在解决大规模复杂问题时的关键技术，它通过函数近似减少了存储需求，提高了学习效率，而且通过梯度下降等优化算法不断改进近似函数，使得在动态和非静态的环境中也能有效地学习最优策略。