程序流程图详解：二分法、牛顿法与最小二乘拟合

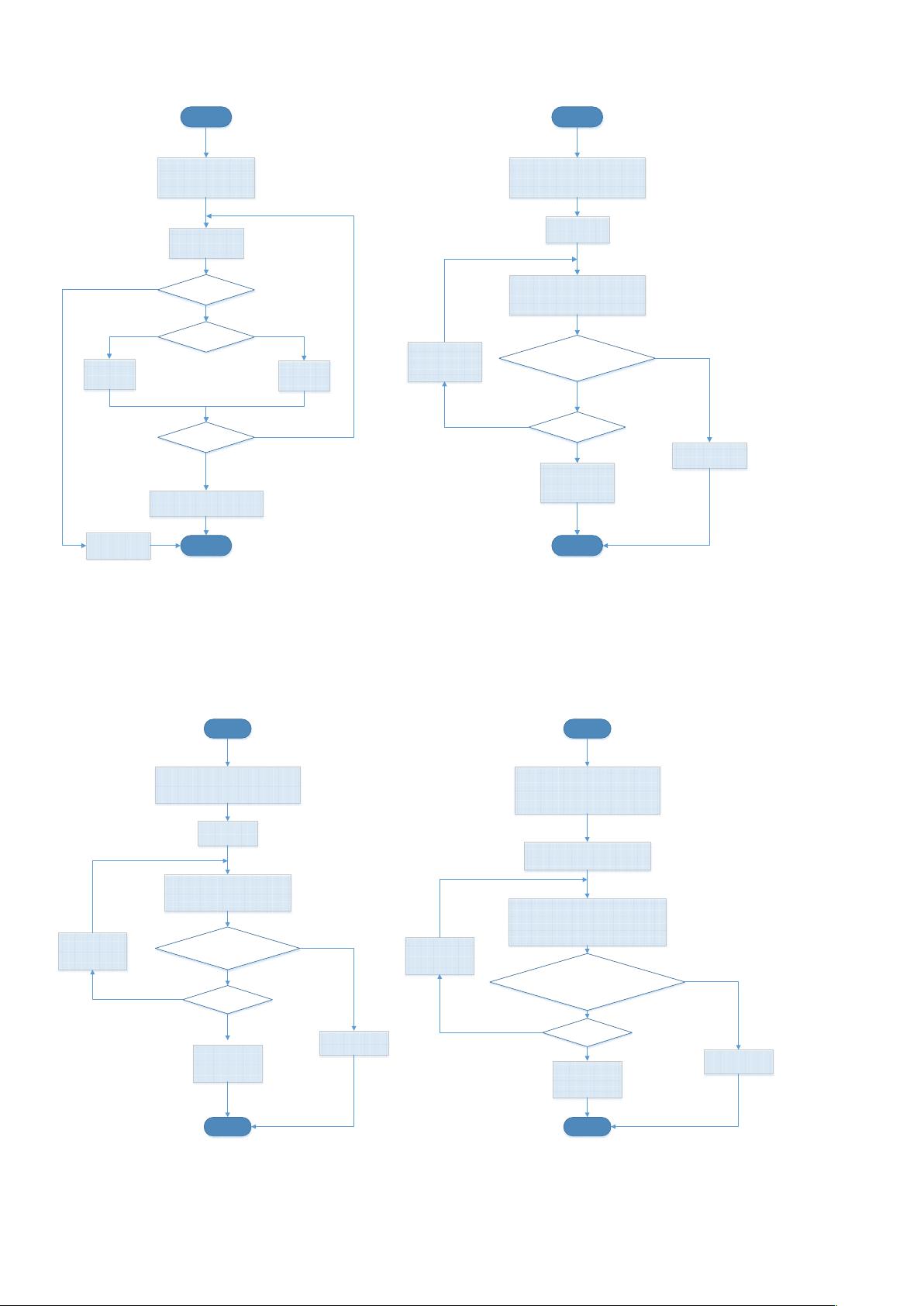
程序流程图1展示了几种数值方法在解决数学问题时的基本步骤，包括但不限于二分法、牛顿（下山）法、割线法、逆Broyden法（或拟牛顿法）、高斯（列主元）消元法和最小二乘拟合。让我们逐一探讨这些方法： 1. **二分法**：用于寻找零点问题的近似解，通过不断将区间缩小，直到找到满足精度条件的解。起始时，设定区间的中点c，并检查f(a)与f(c)的乘积，若异号则更新a和b，重复此过程直到区间长度小于2*delta。 2. **牛顿-下山法**：迭代优化过程，从初始值X0出发，通过迭代更新X的新值X_new，利用导数信息调整步长，直至达到精度delta或者达到最大迭代次数N。如果达到极限，输出X_new。 3. **割线法**：也属于数值搜索方法，每次迭代通过线性插值计算下一个可能的解X(i+1)，直到满足精度要求或达到迭代次数限制。 4. **逆Broyden法**：用于非线性方程组的求解，通过构建并更新一个逆Hessian矩阵来逼近解。当新旧解之间的差异满足精度条件时，更新解向量，直到达到最大迭代次数。 5. **高斯主元消元法**：用于求解线性方程组，通过一系列行交换和消元操作，将系数矩阵变为阶梯形式，然后通过回代求解未知数。若发现方程组奇异，会输出相应的标志。 6. **最小二乘拟合**：处理数据拟合问题，通过构造方程矩阵和右向量，用高斯列主元法求解，得到最优多项式模型，用来描述数据趋势。 7. **Romberg积分法**：一种数值积分方法，对区间[a,b]上的函数f进行精确估计，通过递归地使用梯形法则和Simpson法则的结合，提高精度，直至达到给定的精度delta。 这些流程图展示了各种数值算法的核心思想和执行过程，它们在科学计算、工程优化和数据分析等领域有着广泛的应用。理解并掌握这些方法对于编程、数学建模和解决实际问题具有重要意义。