掌握二叉树:数据结构详解
版权申诉
34 浏览量
更新于2024-07-04
收藏 2.8MB DOC 举报
在《计算机软件基础》多媒体教程的第四章“数据结构”中,着重讲解了二叉树这一重要概念。二叉树是一种特殊的树形数据结构,每个节点最多有两个子节点,通常被分为左子节点和右子节点。这种结构规定了每个节点的后件顺序,如果左子节点先于右子节点,那么它被称为有序二叉树,简称二叉树。
二叉树的表示方式多种多样,其中Backus描述法是常见的两种形式之一。它采用嵌套括号的方式,如A(B(C,D),E(F,)),这种表示法清晰地展示了树的层次关系和节点间的连接。在Backus描述法中,每个节点都有一个根,根后面紧跟其子树的描述,子树又由左子树和右子树组成。
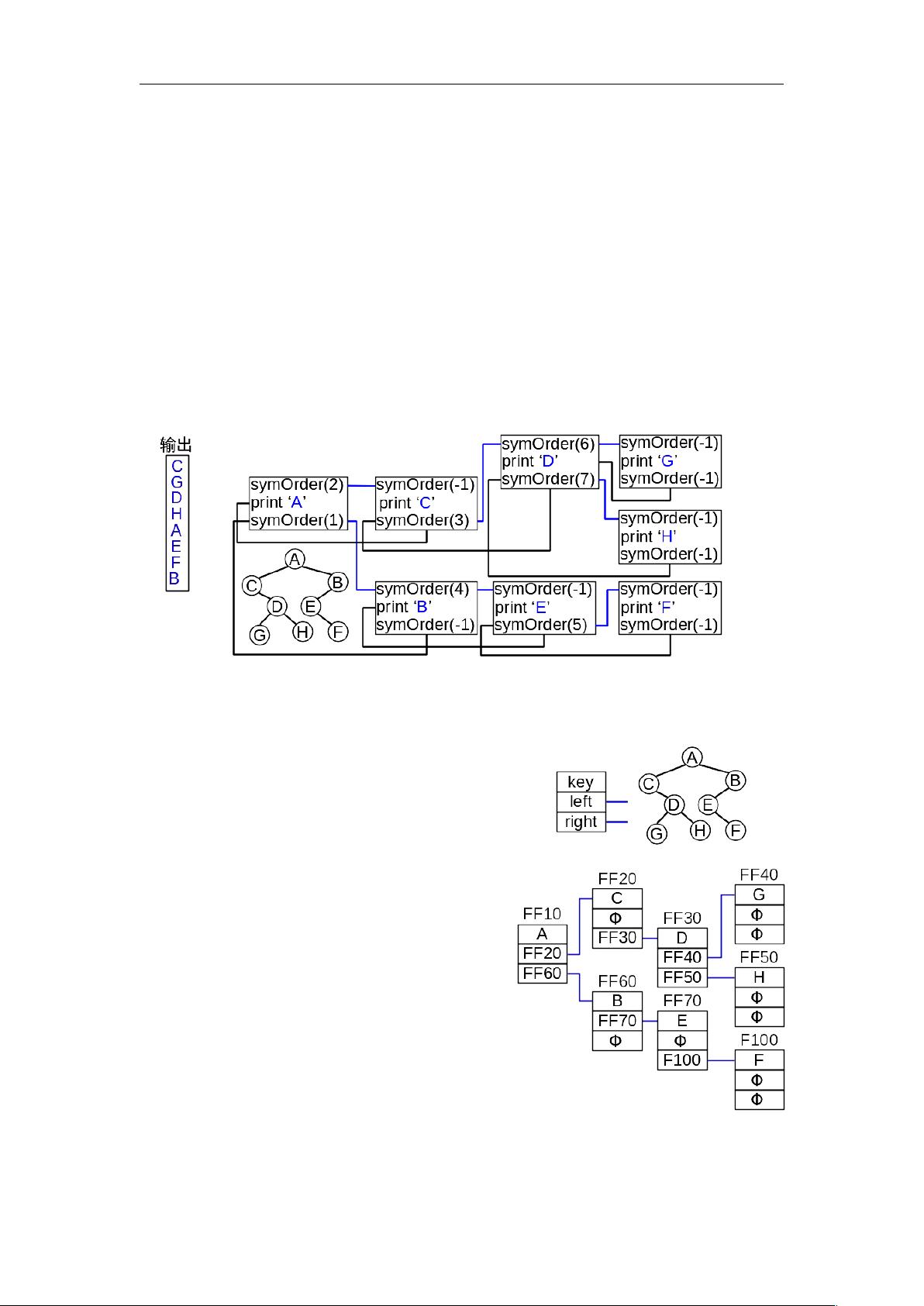
对于二叉树的存储形式,有标准形式和逆形式两种。标准形式通过设置两个指针,pLeftk和prightk,分别指向左子节点和右子节点,使得树的结构可以通过这两个指针得以表示。而在逆形式中,使用一个指针pprek来表示父节点,这样可以更方便地追踪节点之间的父子关系。为了综合这两种优点,还有扩充的标准形式,即同时包含pprek、pLeftk和prightk,这有助于在内存中高效地存储和操作二叉树。
举例来说,一张具体的二叉树存储表格显示了节点的编号、父节点指针以及左右子节点指针,如10节点的左子节点为20,右子节点为60,而20节点的父节点为10等。通过这些信息,我们可以构建和遍历整个二叉树结构。
二叉树在计算机科学中有着广泛的应用,如搜索算法(如二叉搜索树)、排序(如AVL树和红黑树)以及数据压缩(哈夫曼编码)等领域。理解二叉树的基本概念和操作是深入学习数据结构的关键,对后续的算法设计和实现具有重要意义。掌握二叉树的理论和实践应用,能够帮助开发者更有效地处理复杂的数据组织和查询问题。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2022-05-08 上传
2022-11-30 上传
2022-05-08 上传
2022-06-15 上传
2021-09-17 上传
2022-06-12 上传
wxg520cxl
- 粉丝: 25
- 资源: 3万+
最新资源
- JHU荣誉单变量微积分课程教案介绍
- Naruto爱好者必备CLI测试应用
- Android应用显示Ignaz-Taschner-Gymnasium取消课程概览
- ASP学生信息档案管理系统毕业设计及完整源码
- Java商城源码解析:酒店管理系统快速开发指南
- 构建可解析文本框:.NET 3.5中实现文本解析与验证
- Java语言打造任天堂红白机模拟器—nes4j解析
- 基于Hadoop和Hive的网络流量分析工具介绍
- Unity实现帝国象棋:从游戏到复刻
- WordPress文档嵌入插件:无需浏览器插件即可上传和显示文档
- Android开源项目精选:优秀项目篇
- 黑色设计商务酷站模板 - 网站构建新选择
- Rollup插件去除JS文件横幅:横扫许可证头
- AngularDart中Hammock服务的使用与REST API集成
- 开源AVR编程器:高效、低成本的微控制器编程解决方案
- Anya Keller 图片组合的开发部署记录