基于CORDIC算法的数字鉴相方法研究与FPGA实现

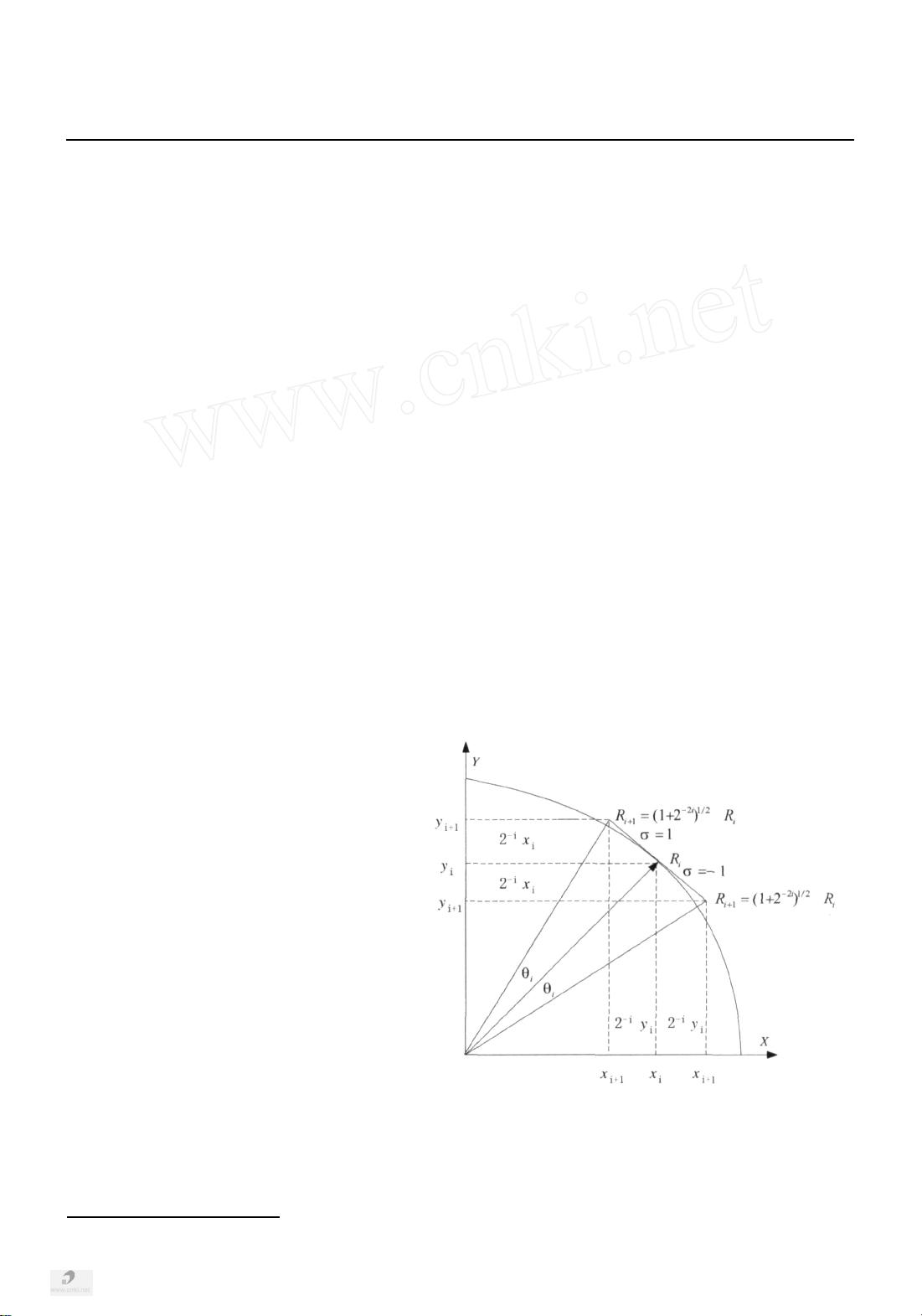
"CORDIC算法研究与实现，用于数字鉴相方法，具有抗噪和抗正交两路失衡性能，适用于FPGA实现" 正文: CORDIC算法是一种经典的坐标旋转数字计算方法，由John Volder在1959年首次提出。它的主要应用在于进行坐标变换，后来逐渐发展为一个通用的数学运算工具，能够处理乘法、除法、平方根、三角函数以及复数运算等多种计算任务。这种算法的独特之处在于它仅依赖于简单的移位和加法操作，使得它非常适合于硬件实现，特别是FPGA（现场可编程门阵列）等数字逻辑设备。 在数字鉴相领域，CORDIC算法通过将输入的正交信号I和Q转化为极坐标形式，从而计算出信号的相位。其基本工作原理可以概括为：通过一系列小角度的迭代旋转，逐步调整初始坐标点的位置，直到达到目标角度。这些小角度是预先设定好的，通常为二进制补码表示的黄金分割角度，这样可以确保每次迭代都是通过对坐标轴进行简单位移来实现的。 在抗噪和抗正交两路失衡性能方面，CORDIC算法表现出良好的鲁棒性。由于其迭代过程对输入数据的敏感度较低，它可以适应噪声环境下的数据处理，同时，对于正交两路信号的不均衡，CORDIC算法也能有效地进行校正。通过精确控制迭代次数，可以实现对计算精度的调整，以适应不同的系统需求。 在FPGA实现中，为了满足实时计算的要求，通常会采用流水线结构，即将算法的不同阶段并行处理，提高处理速度。实验结果表明，相对于传统的查表方法，CORDIC算法能够在保持计算精度的同时，提高运算速度，并有效利用硬件资源，因此在实际应用中具有较高的性价比。 文献标识码A的文章指出，CORDIC算法的广泛应用得益于各大半导体公司如Altera和Xilinx提供的IP核支持。这些IP核允许设计者根据具体应用需求选择合适的CORDIC实现，简化了设计流程，促进了CORDIC算法在各类数字系统中的广泛采用。 CORDIC算法是一种高效且灵活的数值计算方法，尤其适用于需要快速、高精度计算的实时系统，如通信、信号处理等领域。通过深入理解和巧妙应用，可以充分发挥其在硬件实现上的优势，实现复杂数学运算的高效化和小型化。