线性系统的频域分析：频率特性与稳定性

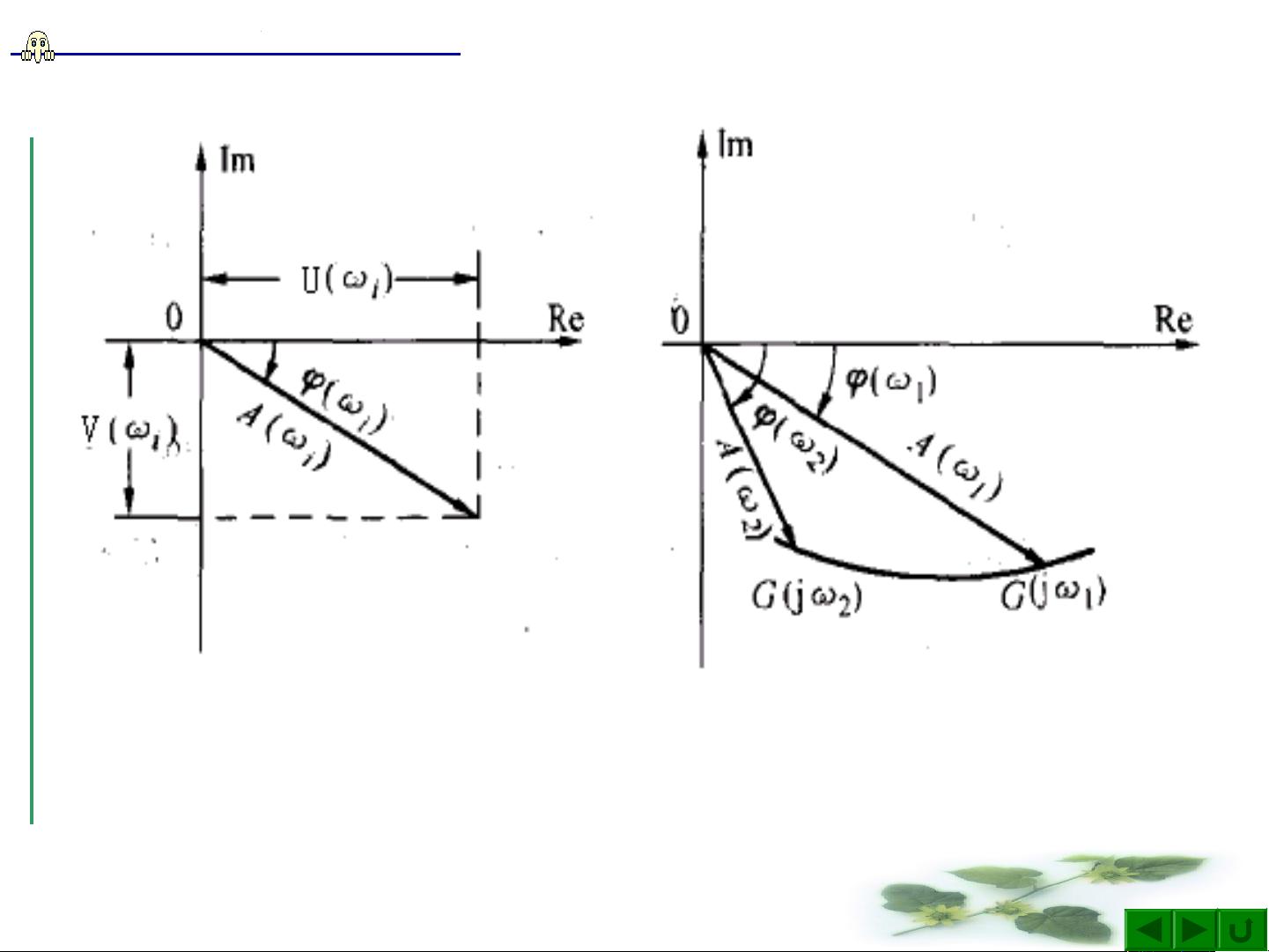
"频率相频幅频" 在控制理论中，频率法是一种常用的技术，用于分析和设计线性系统的性能。这种技术主要应用于C#编程环境中，通过对系统在不同频率下的响应来评估其动态特性。频率法的核心是研究系统的频率特性，这涉及到系统开环和闭环的频率响应。 5-2 典型环节的频率特性 系统中的典型环节，如惯性环节（RC电路）、比例环节、积分环节和微分环节等，都有特定的频率响应。以惯性环节为例，它由电阻R和电容C组成，当输入信号是正弦波时，输出信号会具有不同的幅值和相位，这是由于电容对高频信号的阻抗较低，导致相位滞后。这种环节的频率特性可以表示为G(s) = 1/(1 + sRC)，其中s是复频变量，频率特性则体现在实部（幅频特性）和虚部（相频特性）上。 5-3 系统开环频率特性的绘制 系统开环频率特性通过Bode图（幅频和相频曲线）来描绘，这有助于理解系统对不同频率输入的响应。幅频特性显示了增益（即输出与输入之比的dB值）随频率的变化，而相频特性则揭示了输出相对于输入的相位差。 5-4 奎斯特稳定判据和系统的相对稳定性 乃奎斯特判据是判断线性时不变系统稳定性的重要工具。通过分析开环系统的幅值和相位在复平面上的轨迹，可以确定系统闭环后的稳定状态。如果轨迹包围了-180度的相角点（即单位圆）一圈或多圈，则系统不稳定；反之，如果未包围，则系统稳定。 5-5 系统的频率特性及频域性能指标 系统性能通常通过频域指标来衡量，包括上升时间、峰值时间、超调量、稳态误差等。这些指标可以从频率特性中推导，帮助工程师优化系统设计。 5-6 频率特性的实验确定方法 除了理论计算，频率特性也可以通过实验方法获取，例如扫频振荡法、傅里叶变换等。实验数据有助于验证理论计算的准确性，并且能反映实际环境中的系统行为。 5-7 MATLAB进行系统的频域分析 MATLAB提供了强大的工具，如控制系统工具箱，用于进行系统的频域分析。用户可以利用这些工具绘制Bode图、Nyquist图和Nichols图，进行稳定性分析和系统校正。 频率法在工程实践中非常实用，因为它提供了直观的图解方式来理解和调整系统性能。通过对系统频率特性的深入理解，工程师能够更好地设计和优化C#编程中的控制算法，确保系统的稳定性和性能满足预期。