倒立摆系统Lagrange方程建模与模糊控制方法

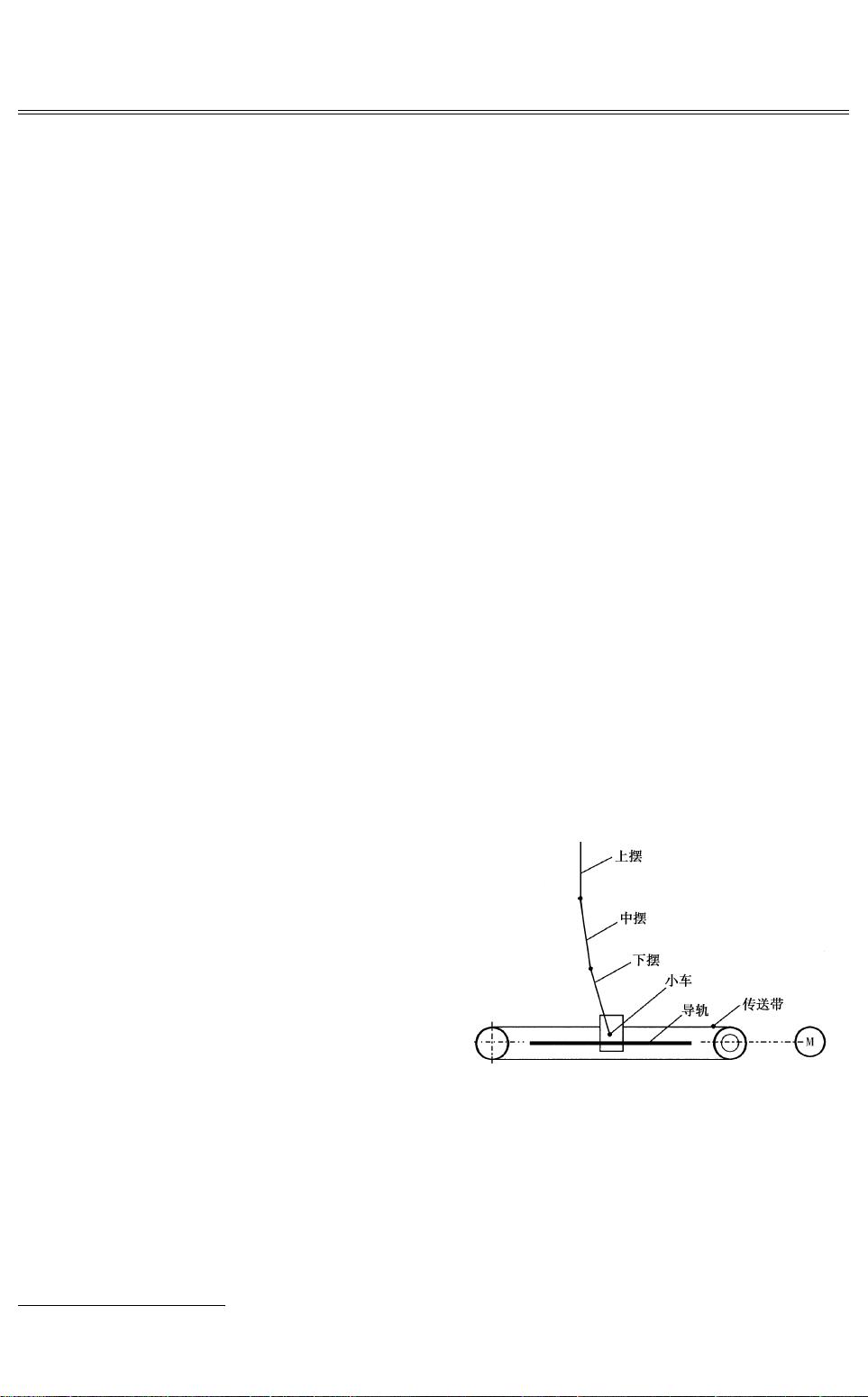
"这篇论文是2002年的自然科学论文，由宋君烈、肖军和徐心和共同撰写，得到了国家自然科学基金的支持。研究主要关注倒立摆系统的建模和控制，特别是通过Lagrange方程进行动力学建模，并提出了一种模糊控制策略。该方法降低了建模复杂性，并在仿真和实际物理系统实验中验证了控制方法的有效性。倒立摆系统作为非线性、多变量和强耦合的不稳定系统，是控制理论研究的重要对象，涉及镇定、非线性、鲁棒性等多个关键问题。论文中，作者们利用Lagrange方程的优势，即简化微分方程组的求解和排除约束反力的影响，来建立系统的数学模型。" 这篇论文深入探讨了倒立摆系统的动态建模和控制策略。倒立摆系统由于其多变量、非线性和强耦合的特性，对控制理论提出了严峻挑战。传统的牛顿运动定律建模方法会涉及到复杂的微分方程组求解，且需考虑约束条件，这使得建模变得困难。为了解决这个问题，论文引入了Lagrange方程，这是一种分析力学的方法，它允许用广义坐标来表示系统的运动方程，方程的数量与系统的自由度一致，且不需考虑理想约束反力，简化了建模过程。 论文中提出的模糊控制方法基于模糊组合变量，这种控制策略在处理倒立摆系统这类非线性系统的控制问题时，能够有效应对不确定性，提高控制性能。通过仿真研究和实际物理系统实验，该模糊控制方法被证实能够有效地稳定倒立摆系统，显示出其在解决复杂控制问题上的潜力。 此外，倒立摆系统的控制也涉及到其他关键问题，如系统的镇定、非线性控制、鲁棒性及跟踪问题。这些挑战是控制理论研究的核心，也是倒立摆系统作为研究平台的价值所在。论文引用了前人的研究成果，表明了该领域的研究是持续和广泛的，而提出的Lagrange方程建模与模糊控制相结合的方法，为这一领域的研究提供了一个新的视角和实用工具。 这篇论文展示了Lagrange方程在复杂系统建模中的优势，以及模糊控制在解决非线性控制问题中的有效性，对于理解和改进不稳定系统的控制策略具有重要的理论和实践意义。