MATLAB教程：非线性方程求解与数值计算方法详解

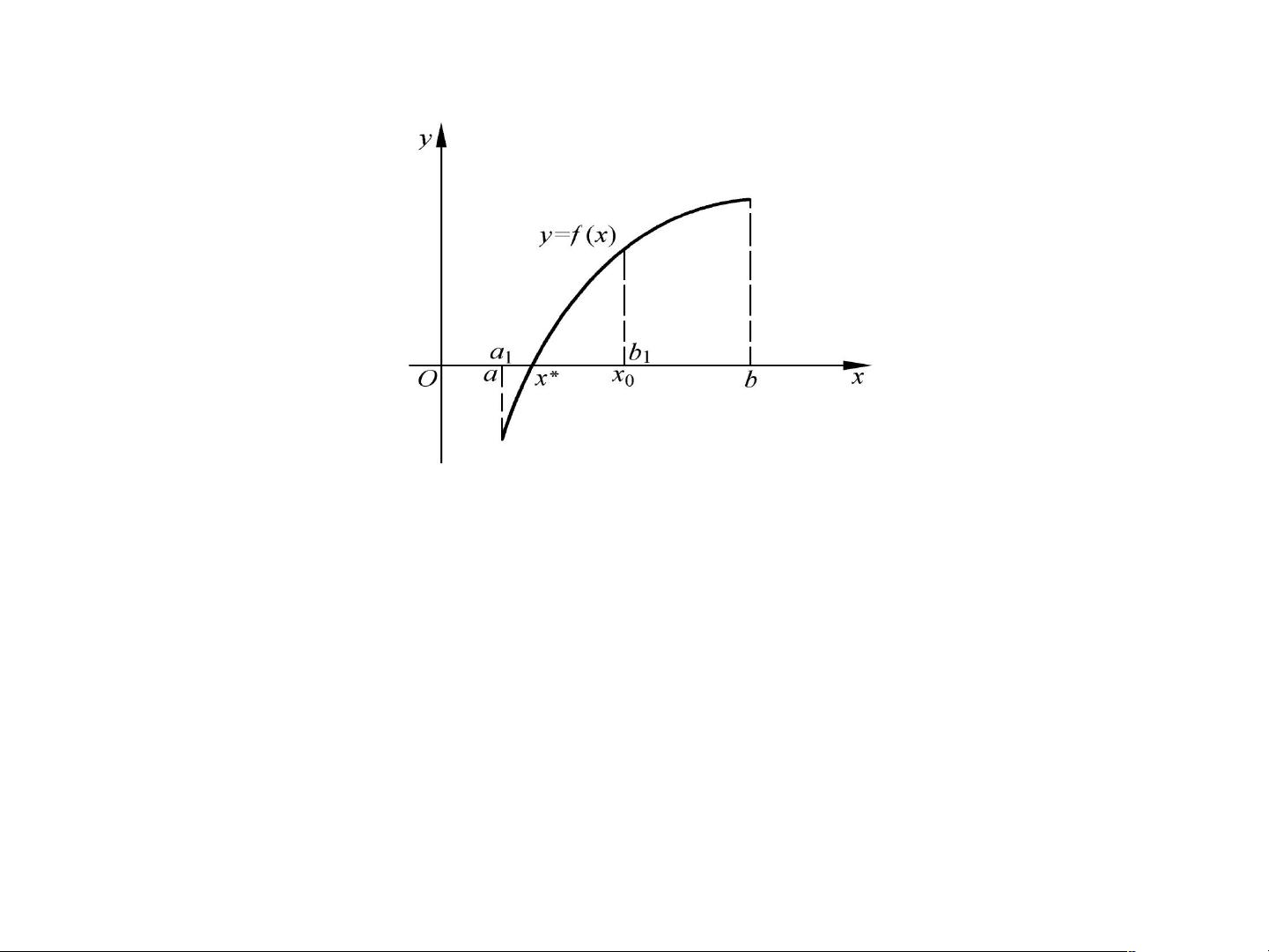
本资源主要讲解基于Matlab的实用数值计算方法，重点聚焦于求解非线性方程。章节四详细介绍了如何利用MATLAB解决形式为f(x)=0的方程，包括两种主要的求解策略：符号法和数值解的基本方法。 1. MATLAB符号法：这种方法适用于求解代数方程和超越方程，通过`solve`指令实现。例如，`z = solve(s,'v')`命令中，`s`代表待解方程，`v`则是对应未知量，可以处理任意复杂的超越方程。但需要注意的是，不是所有方程都能直接通过符号法得到解析解，对于复杂的方程，可能需要借助数值算法。 2. 数值解的基本方法：这部分内容涵盖了多种数值求解技术，如： - 二分法：适用于函数在给定区间单调且连续的方程，通过不断缩小区间的中点判断根的位置，直到达到预设精度。 - 迭代法：这是一种通用的求解方法，通过构造一个序列逼近方程的根，如牛顿法、高斯-赛德尔法等。 - 切线法：基于函数在某点的切线来估计根的近似值。 - 割线法：结合了切线法和二分法的思想，用于更精确的根搜索。 4.2节中，强调了解决非线性方程可能存在无法通过符号法求解的情况，这时数值方法就显得尤为重要。通过这些数值算法，用户可以找到方程的近似解，这对于实际工程问题的求解具有很高的实用价值。 此外，章节还提供了实际操作的练习，如编写代码`ex1.m`来求解方程，并要求结果以保留四位有效数字的方式展示，以及通过示例图4-1直观地演示二分法的工作原理。 总结来说，这个课程提供了一套完整的基于Matlab的非线性方程求解工具箱，包括理论概念和实践操作，是学习数值计算和Matlab编程的宝贵资源。