凸优化基础:从凸集到对偶理论
需积分: 11 113 浏览量
更新于2024-07-19
收藏 3.56MB PPT 举报
"这是一份关于凸优化的在线课件,由七月算法的邹博讲解,适合初学者参考。课程涵盖了凸集的基本概念,包括保凸运算、分割超平面和支撑超平面;还介绍了凸函数的特性,如上境图、Jensen不等式以及保凸运算。此外,课程讲解了凸优化的一般方法,如对偶函数、鞍点解释,以及如何利用对偶求解最小二乘问题,并提到了强对偶的KKT条件。"
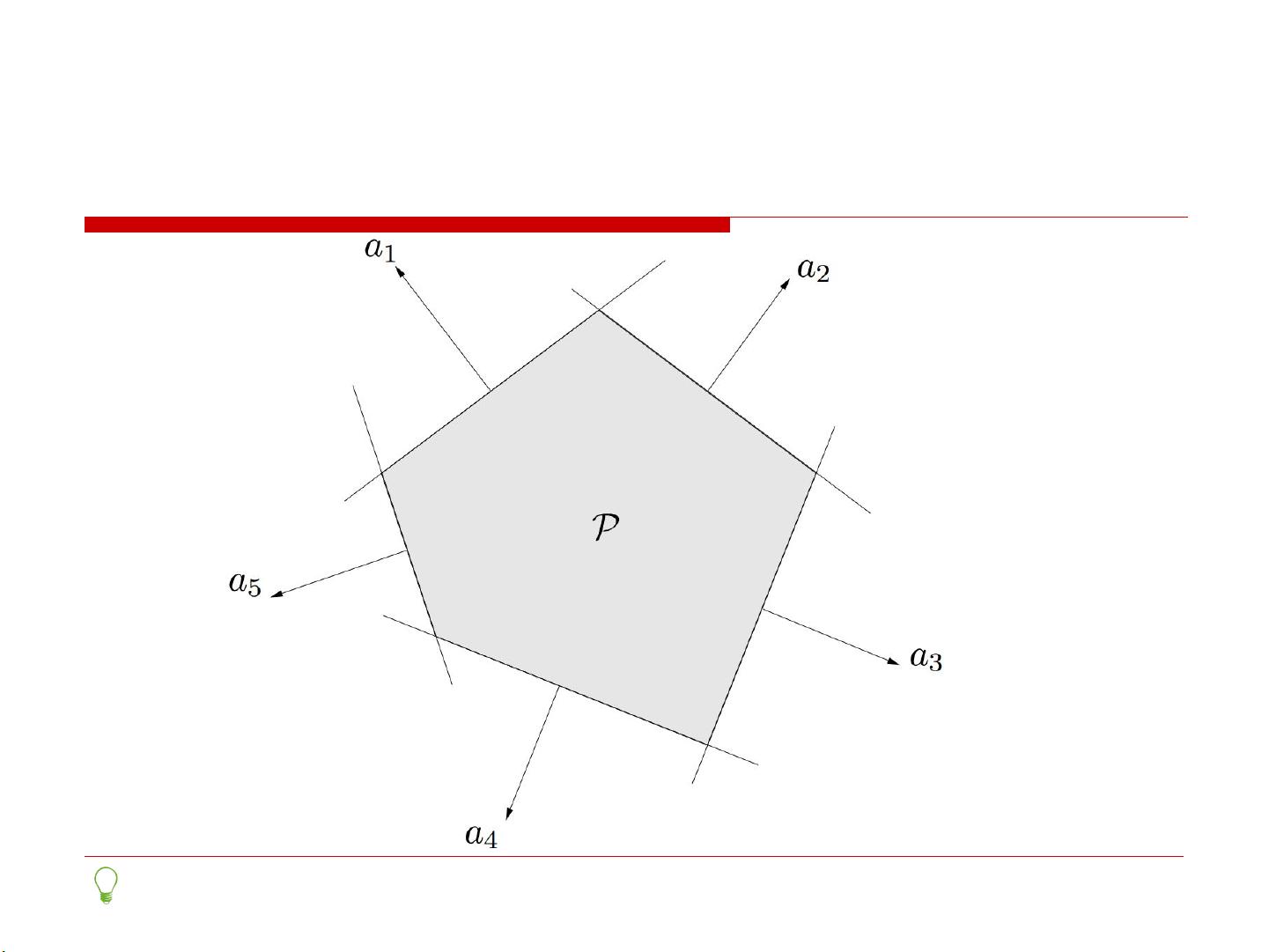
在机器学习领域,凸优化是一个至关重要的主题,因为它能提供全局最优解,避免局部最优的情况。首先,我们来深入理解凸集的概念。一个集合被称为凸集,如果其中任意两点间的线段都完全包含在这个集合内。例如,抛物线y=x^2的上方区域就是一个凸集。接着,课件介绍了超平面和半空间,它们是定义和操作凸集的重要工具。超平面是平面上的一条直线,而半空间则是由超平面一侧的所有点组成的空间。
接着,课程讲解了凸函数,这是凸优化的核心。一个函数如果其图像的上方区域是凸集,那么这个函数就是凸函数。凸函数的特性包括上境图(函数值域的上边界)和Jensen不等式,后者揭示了凸函数在平均值上的行为。此外,凸函数的保凸运算表明,如果一个函数是凸的,那么其某些组合或变形仍将是凸的。
在凸优化问题的求解中,对偶理论扮演了关键角色。对偶函数是从原始问题派生出的辅助函数,可以帮助我们找到原问题的最优解。鞍点解释则是连接原始问题和对偶问题的一种方式,它描述了当原问题和对偶问题的解相等时的平衡状态。课件中还提到了利用对偶求解最小二乘问题的方法,这是机器学习中常见的问题。
最后,KKT条件是强对偶性的充分必要条件,它指出在满足一定条件下,原问题和对偶问题的最优解会同时达到。KKT条件为实际的优化问题提供了理论基础。
这份凸优化课件系统地介绍了凸集和凸函数的基本概念,以及如何利用这些知识解决实际的优化问题,特别是对于机器学习中的模型训练和参数优化具有指导意义。通过深入学习,读者可以掌握优化问题的全局最优求解策略,这对于提升模型性能和理解复杂算法的内在逻辑至关重要。
273 浏览量
248 浏览量
2017-10-20 上传
2018-05-25 上传
159 浏览量
qq_21729293
- 粉丝: 0
- 资源: 2
最新资源
- laravel-simple-order-system
- VulkanSharp:Vulkan API的开源.NET绑定
- 网络游戏-网络中的帧传送方法以及节点、帧传送程序.zip
- bc19-webapp
- bagging算法
- c语言课程设计-职工资源管理系统
- 类似WINDOWS进度复制文件夹例子-易语言
- CPSC471-Project
- uzkoogle
- CBEmotionView(iPhone源代码)
- crunchyroll-ext
- 2016年数学建模国赛优秀论文.zip
- 运输成本估算器:允许用户估算物品的运输成本
- Unrar调用模块 - RAR解压、测试、查看全功能版-易语言
- 鸿蒙轮播图banner.7z
- Mailican-crx插件