递归算法性能优化：内联汇编与斐波那契数列分析

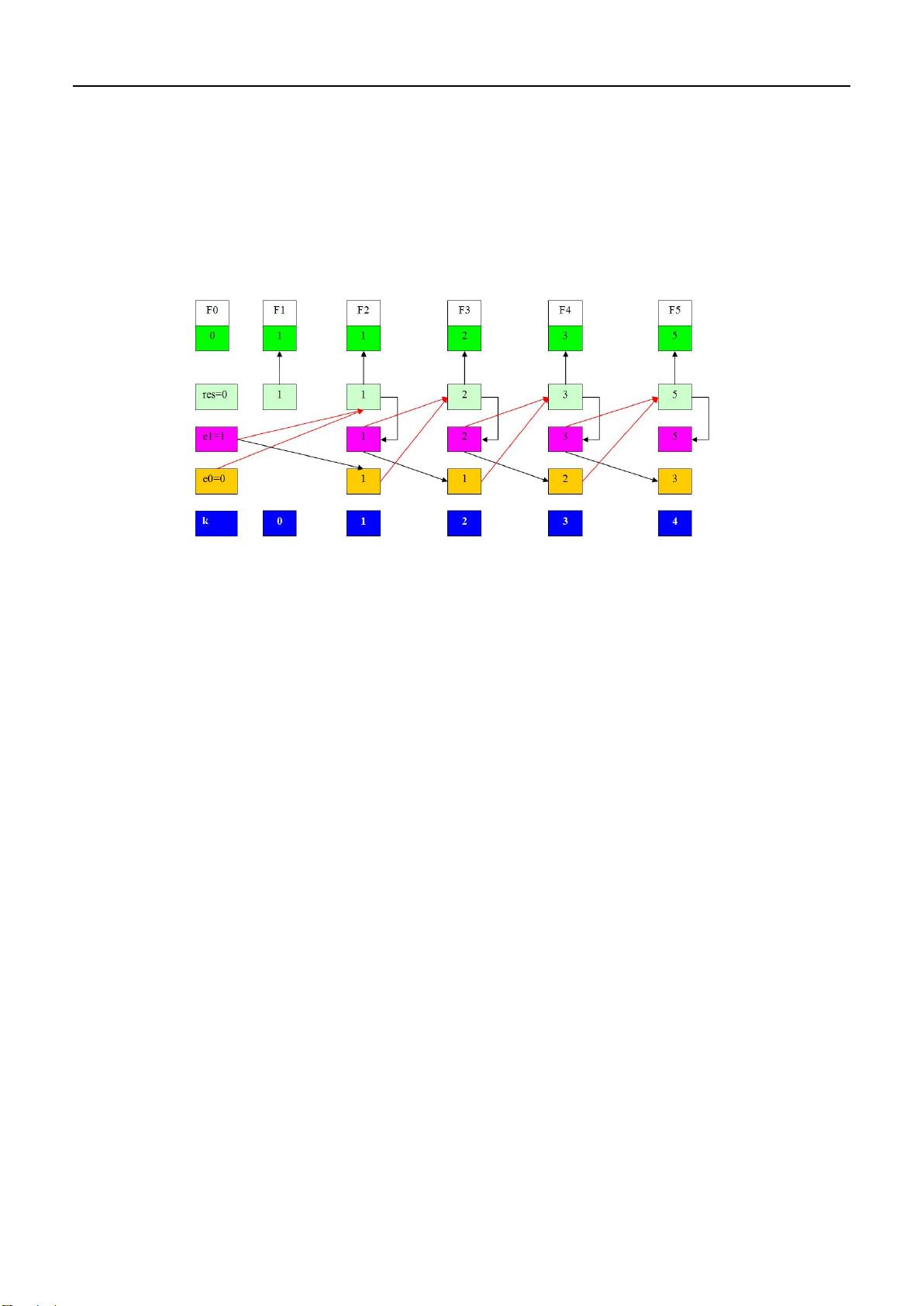
"黎先波的一篇关于汇编语言优化递归算法性能的论文，主要探讨了如何通过内联汇编来提升斐波那契数列计算的效率。" 在计算机科学领域，递归算法是一种常用的问题解决策略，它通过将大问题分解为相同或相似的小问题来求解。递归算法在处理某些特定问题时表现出强大的能力，比如树遍历、图搜索以及本文关注的斐波那契数列。然而，随着信息时代的快速发展，对高性能算法的需求日益增长，传统的递归算法在处理大规模数据时往往效率低下，因为它们会引入大量的重复计算。 斐波那契数列是计算机科学中的一个经典例子，其定义为每个数是前两个数的和，例如：F(0) = 0，F(1) = 1，F(n) = F(n-1) + F(n-2) (n >= 2)。递归实现虽然简洁，但在计算较大值时，由于重复计算次数过多，效率非常低。 论文作者黎先波提出使用内联汇编来优化递归算法的性能。内联汇编允许程序员在高级语言（如C++或C）中嵌入汇编代码，直接对硬件进行低级别操作，以提高程序性能。通过这种方式，可以针对性地优化算法的关键部分，减少不必要的计算和内存访问，从而提升整体运行速度。 汇编语言是与机器硬件直接对应的编程语言，对处理器指令有直接控制权。优化斐波那契数列的递归算法时，可能涉及到以下汇编优化技巧： 1. 缓存利用：优化数据访问模式，减少缓存未命中，提高数据读取速度。 2. 分支预测：避免或减少条件分支，减少处理器流水线的中断。 3. 向量化：利用SIMD（单指令多数据）指令，一次性处理多个数据，提高并行计算能力。 4. 循环展开：增加循环体内的计算量，减少循环次数，减少循环开销。 5. 手动栈管理：精细控制栈空间分配，避免递归调用带来的栈溢出问题。 黎先波的论文很可能详细分析了这些优化技术在斐波那契数列递归算法中的应用，通过实验证明了内联汇编在提升算法性能方面的有效性。这样的研究对于理解底层硬件工作原理、提高软件性能具有重要意义，特别是在需要高效计算的领域，如科学计算、大数据处理和机器学习等。