The relative weight of fs is determined by the image
sensor, so we first decide on it. The image sensor should
have a short exposure time to improve ambient light
rejection (Section II.E), and a large number of pixels for
resolution of x. We chose a global-shutter CMOS sensor
with 752 pixels of resolution and a minimum shutter time
of 35μs. Each pixel is 6μm, and we expect to be able to
resolve the laser dot to within 0.1 pixel or better.
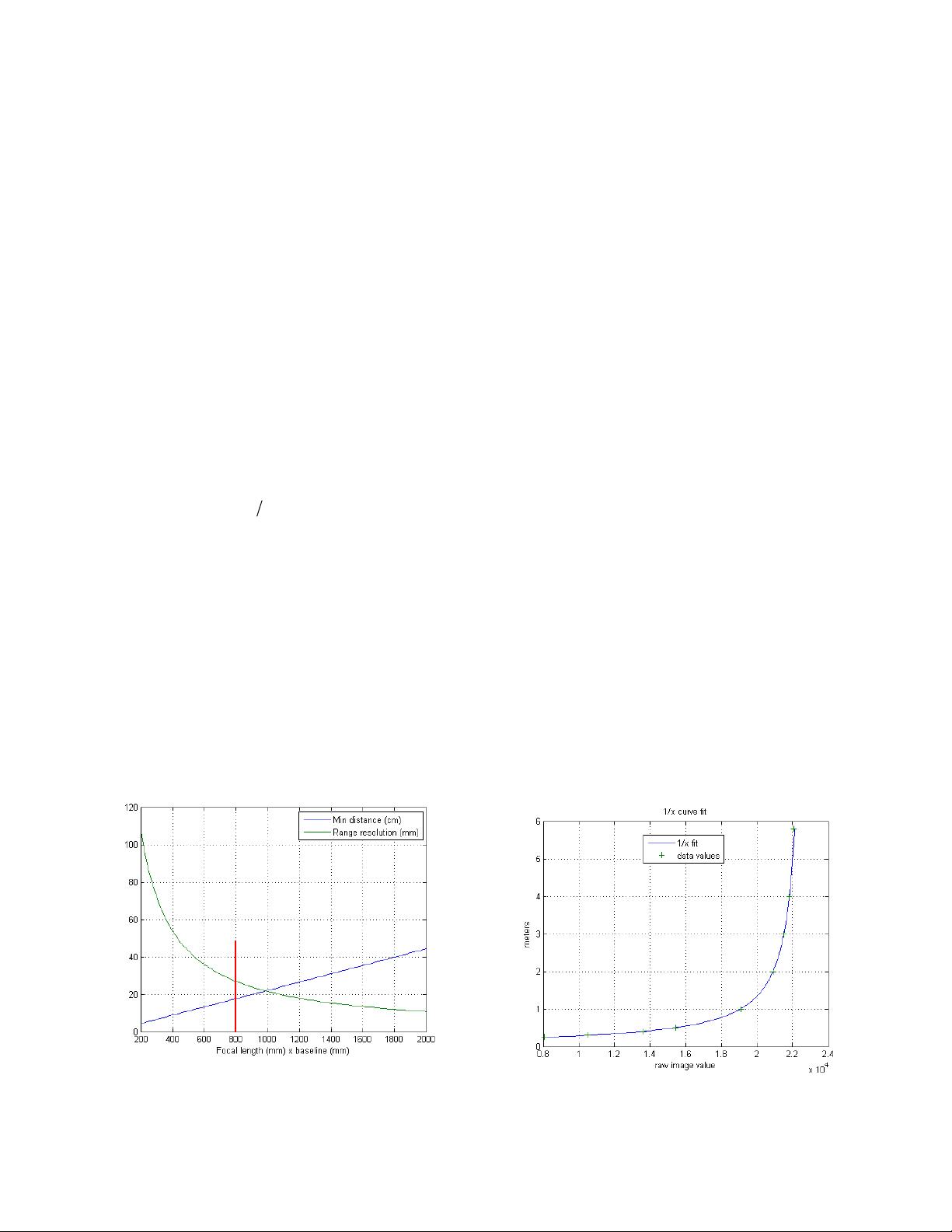
With these parameters, we can plot the effect of fs on
range resolution and min distance (Figure II-2). If the min
distance is to be 20cm or less, fs should be 900 or less. If
the range resolution is to be 30mm or less at 6m, the fs
product should be greater than 700. We pick 800 as the
“sweet spot” for the device.
The product fs = 800 can be achieved in different ways,
but the bias is towards a compact baseline, while keeping
the focal length reasonable (larger focal lengths demand
longer lenses). With a baseline of 50mm, the focal length
is 16mm, and we chose this combination.
Finally we can determine the angle β of the laser
relative to the optical axis:
o
mf 82))6*376(arctan( ≈=
μβ
(4)
C. Module Calibration
The total error of the device is a function of the device
parameters, the error in dot resolution, and the calibration
of the device. Calibration here refers to all the
misalignments that could affect the ideal operation of the
device. Because we are using low-cost optical
components, the design must account for major
inaccuracies. The main ones are laser pointing angle, lens
pointing angle, and lens distortion.
• Laser pointing angle. The laser must point vertically
in a plane parallel to the base of the device, and point
horizontally at an 8 degree angle towards the principal
ray of the camera. Low-cost laser modules have
typical pointing accuracies of at best 6 degrees. We
compensate for pointing angle mechanically, using
laser module rotation and a vertical rotation mount.
• Lens pointing angle. The diagram of Figure II-1
shows the laser beam and the lens principal ray in the
same plane. Generally this will not be the case.
Instead, in calibration we search for the horizontal
scanline that best corresponds to the laser beam at all
distances. We then use 5 scanlines above and below
this central line. If the imager is not rotated too much
relative to the plane of the laser and focal point, these
lines are sufficient to approximate the ideal planar
geometry.
• Lens distortion. For a low-cost 16mm lens, the
distortion will be at least a few percent at the edge of
field, even when optimizing for a single wavelength.
This is enough to be the major error in distant
readings, and must be compensated.
We use a two-step calibration process to deal with lens
distortion. First, we fit a 1/x curve using the following
procedure.
• Localize the laser dot image to subpixel accuracy
(Section II.D).
• For a set of readings at known distances, fit the ideal
curve of Eq. 1, weighting distant readings more
heavily. There are two parameters to be optimized:
the product fs, and the pixel offset for calculating x.
The 1/x fit yields the curve of Figure II-3. While the data
points seem to lie well on the curve, the steep slope at
larger distances means that small deviations result in large
calibration errors (Equation 3). Figure II-4 shows the
errors due only to the 1/x curve fit, at different distances.
Both the sensitivity of distance to pixel errors, and the
amount of pixel error from distortion, increase at larger
distances (towards the edge of the imager). Note that
calibration errors at distances less than 1m are less than
2mm.
Figure II-2 Min distance and Range resolution relative to fs. The design
criteria is to keep min distance less than 20cm, and range resolution less
than 40mm. The vertical line is a sweet spot.
Figure II-3 1/x calibration curve. The raw image value is the pixel value
of the centroid of the laser dot, interpolated to 1/32 pixel.
3004
Authorized licensed use limited to: Guangdong Univ of Tech. Downloaded on January 19, 2010 at 08:56 from IEEE Xplore. Restrictions apply.









