动态查找与二叉排序树

“数据结构教学课件：第19讲 动态查找.pdf” 本文主要讨论的是数据结构中的动态查找技术，特别是通过二叉排序树（二叉查找树）实现动态查找的方法。动态查找表是一种在查找过程中根据需要动态生成表结构的数据结构。当查找某个值Key时，如果表中存在匹配的关键字记录，则查找成功；若不存在，就将Key插入到表中。 9.3动态查找表是一个关键概念，它强调了查找过程中表的动态构建。在动态查找表中，如果要查找的键值不存在，系统会自动将其插入到表中，从而保持表的某种特定顺序，例如在二叉排序树中，这种顺序是有序的。 二叉排序树是一种特殊的二叉树，满足以下特性： 1. 如果它是空树，那么它满足条件。 2. 如果其左子树非空，左子树上的所有节点的值都小于根节点的值。 3. 如果其右子树非空，右子树上的所有节点的值都大于根节点的值。 4. 它的左子树和右子树也都是二叉排序树。 二叉排序树的一个重要特性是中序遍历，它能生成一个递增的关键字序列。例如，给定的二叉排序树在中序遍历后得到序列3, 12, 24, 37, 45, 53, 61, 78, 90, 100。 在二叉排序树中进行查找，通常遵循以下步骤： 1. 如果查找的值等于根节点的关键字，查找成功。 2. 如果查找值小于根节点的关键字，继续在左子树查找。 3. 如果查找值大于根节点的关键字，继续在右子树查找。这个过程在左右子树上递归进行。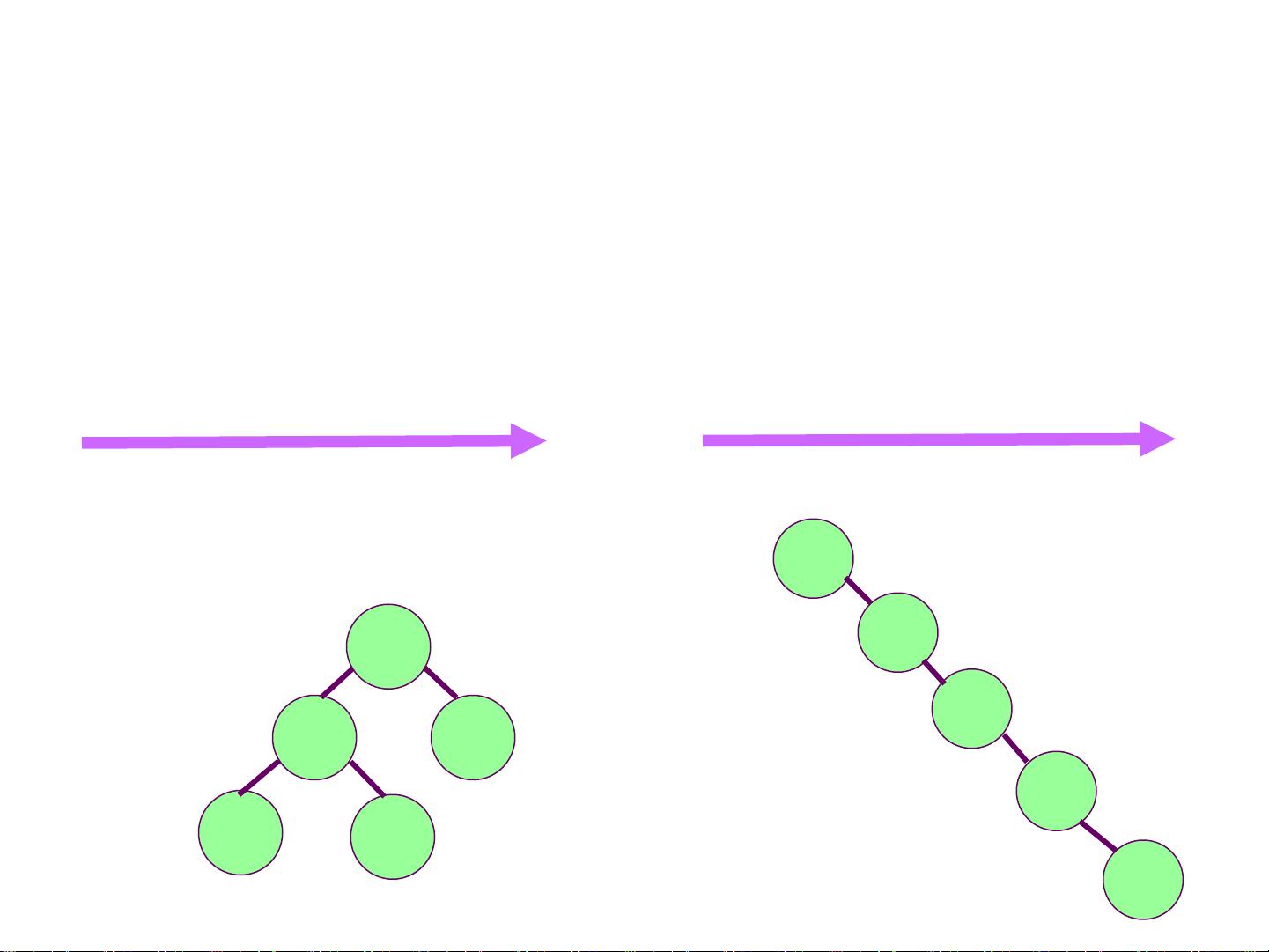 在不同的插入次序下，二叉排序树的形态会有所不同，这直接影响到平均查找长度（ASL）。例如，等概率下，一种插入次序可能导致ASL为(2n+2)/5，而另一种插入次序可能导致ASL为(3n+5)/5。最坏情况下，ASL可以达到(n+1)/2，与顺序查找相同；而在最好的情况下，ASL为log2n，类似于折半查找的判定树。 二叉排序树的插入操作： 1. 若树为空，新插入的节点成为新的根节点。 2. 否则，持续在其左子树或右子树查找，直到找到一个空的子树位置，新节点将作为该空子树的左孩子或右孩子。 举例来说，如果要在给定的二叉排序树中插入数值“20”，我们会发现它小于根节点45，因此我们进入左子树，接着小于37，再进入24的左子树，由于24的左子树为空，20将被插入作为24的左孩子，形成新的二叉排序树。 动态查找表和二叉排序树在数据结构中占有重要地位，它们提供了高效查找和插入操作的能力，尤其是在大数据分析和数据挖掘中，这种效率对于处理大量数据至关重要。理解并熟练掌握这些概念和技术，能够帮助开发者优化算法，提高程序性能。