左倾红黑树算法详解与实现

"这篇资料主要探讨了红黑树这一数据结构的算法，特别是引入了一种左倾红黑树（Left-Leaning Red-Black Trees）的概念，由Robert Sedgewick教授在2008年的两次会议上提出。左倾红黑树被认为是对传统红黑树的一种简化实现，具有完整的删除操作。此外，资料还提到了回归平衡的4节点以及与2-3树的关系，以及对红黑树的科学分析。同时，提供了Java代码和动态演示来辅助理解。" 红黑树是一种自平衡二叉查找树，它在保持二叉查找树特性的同时，通过颜色属性（红色或黑色）确保树的平衡性，从而优化查找、插入和删除操作的时间复杂度。通常，红黑树的每个节点都带有颜色属性，遵循以下性质： 1. 每个节点要么是红色，要么是黑色。 2. 根节点是黑色。 3. 所有叶子节点（NIL或空节点）是黑色。 4. 如果一个节点是红色，则它的两个子节点必须是黑色。 5. 对每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数量的黑色节点。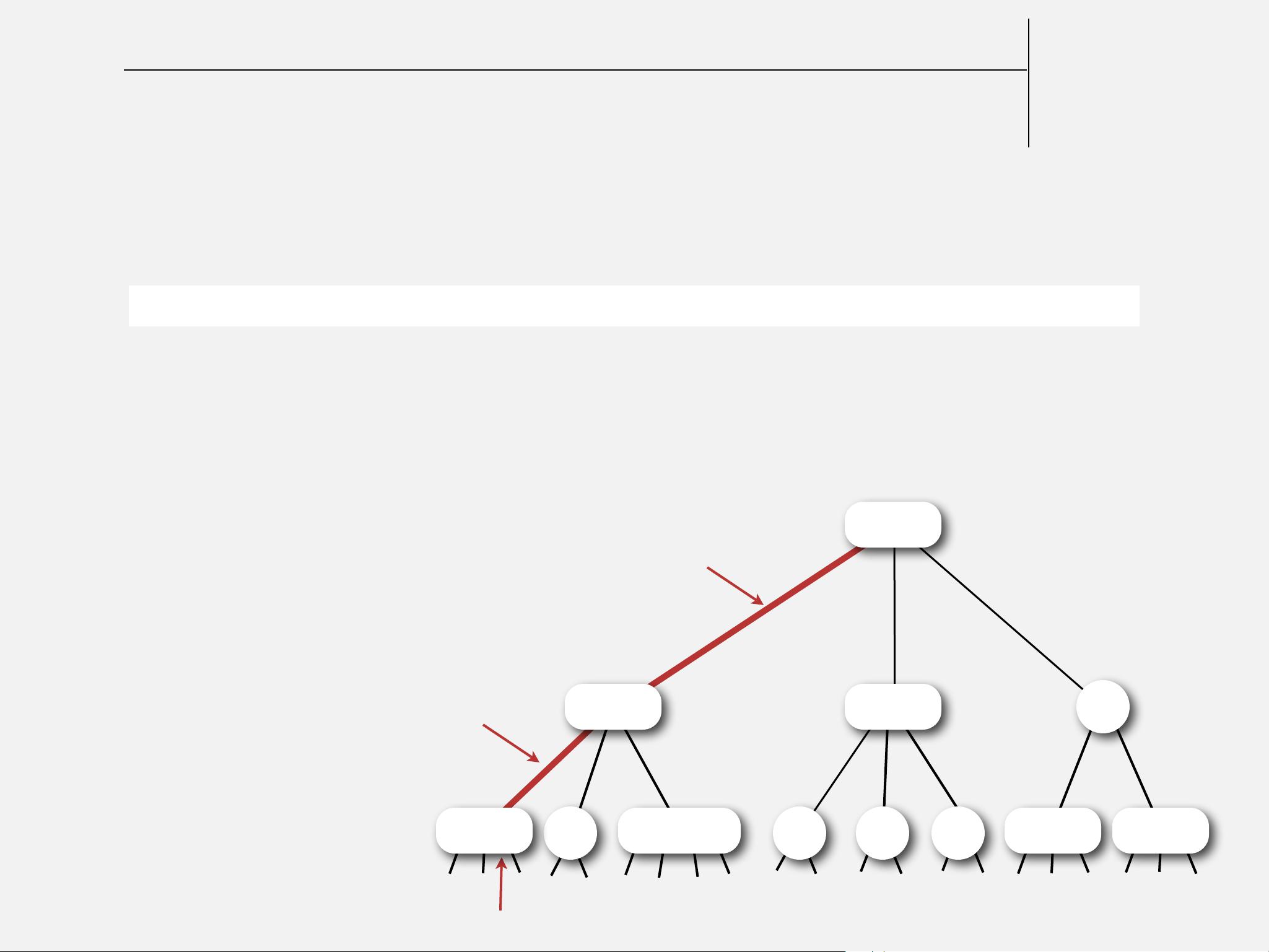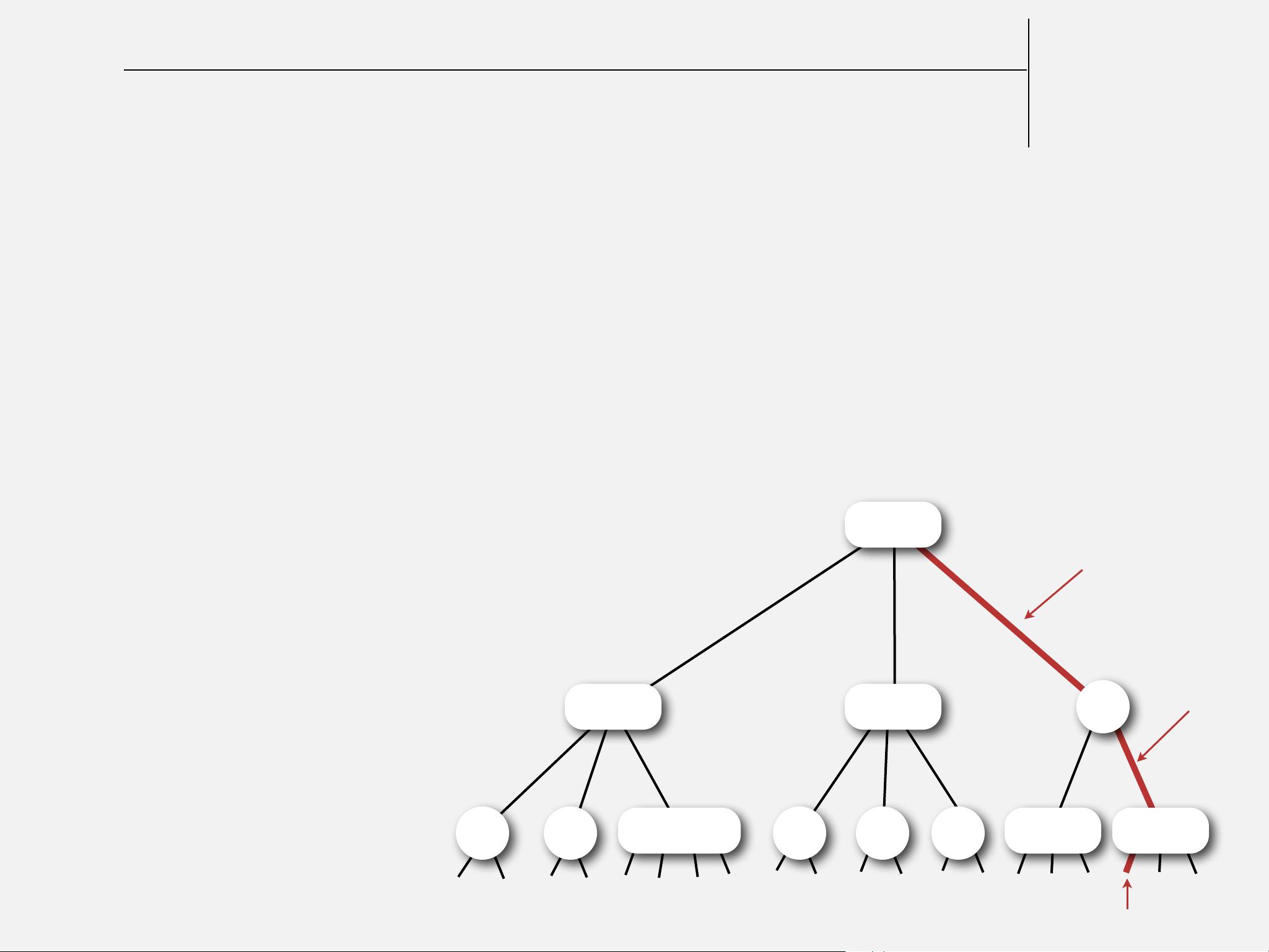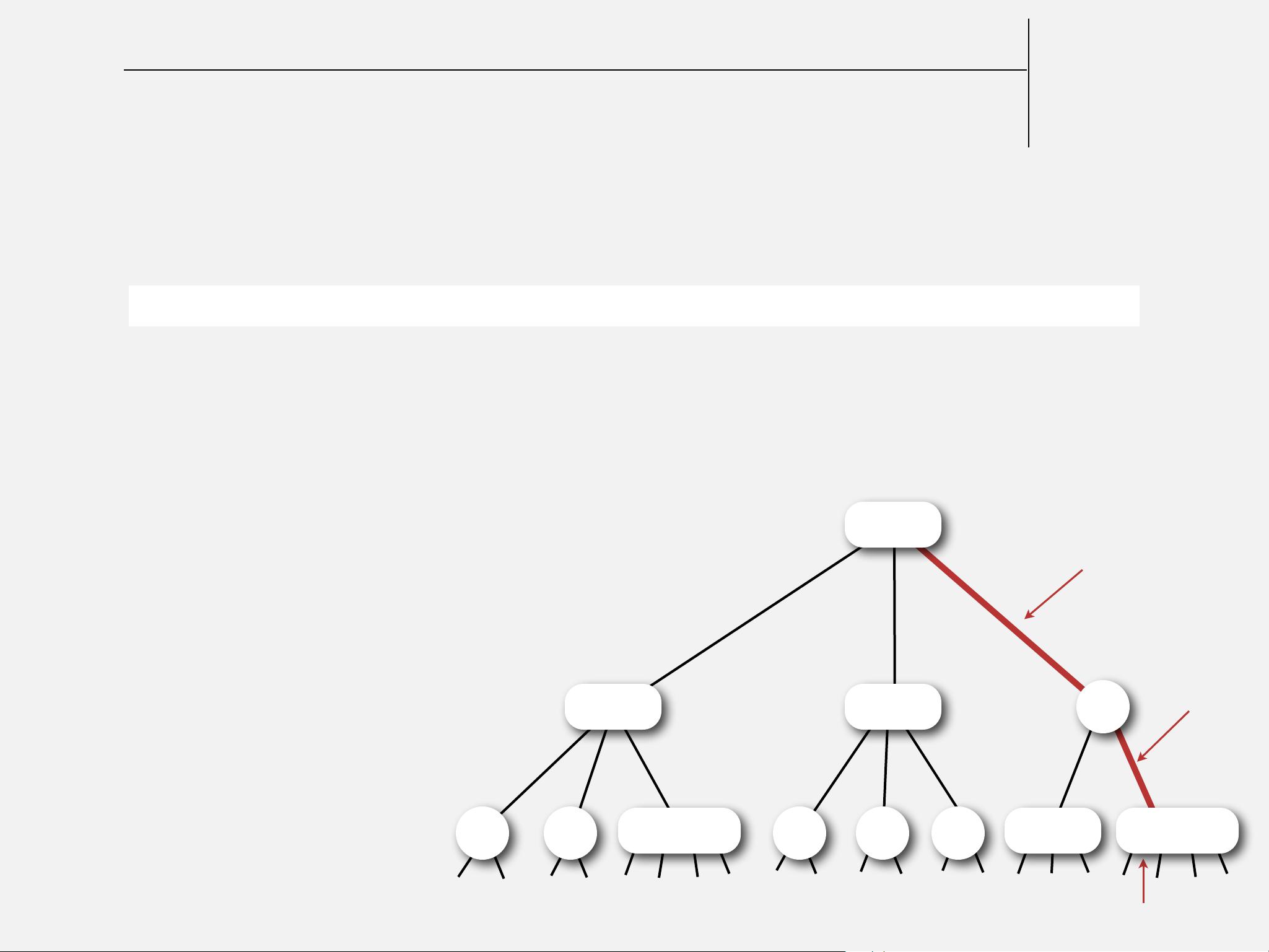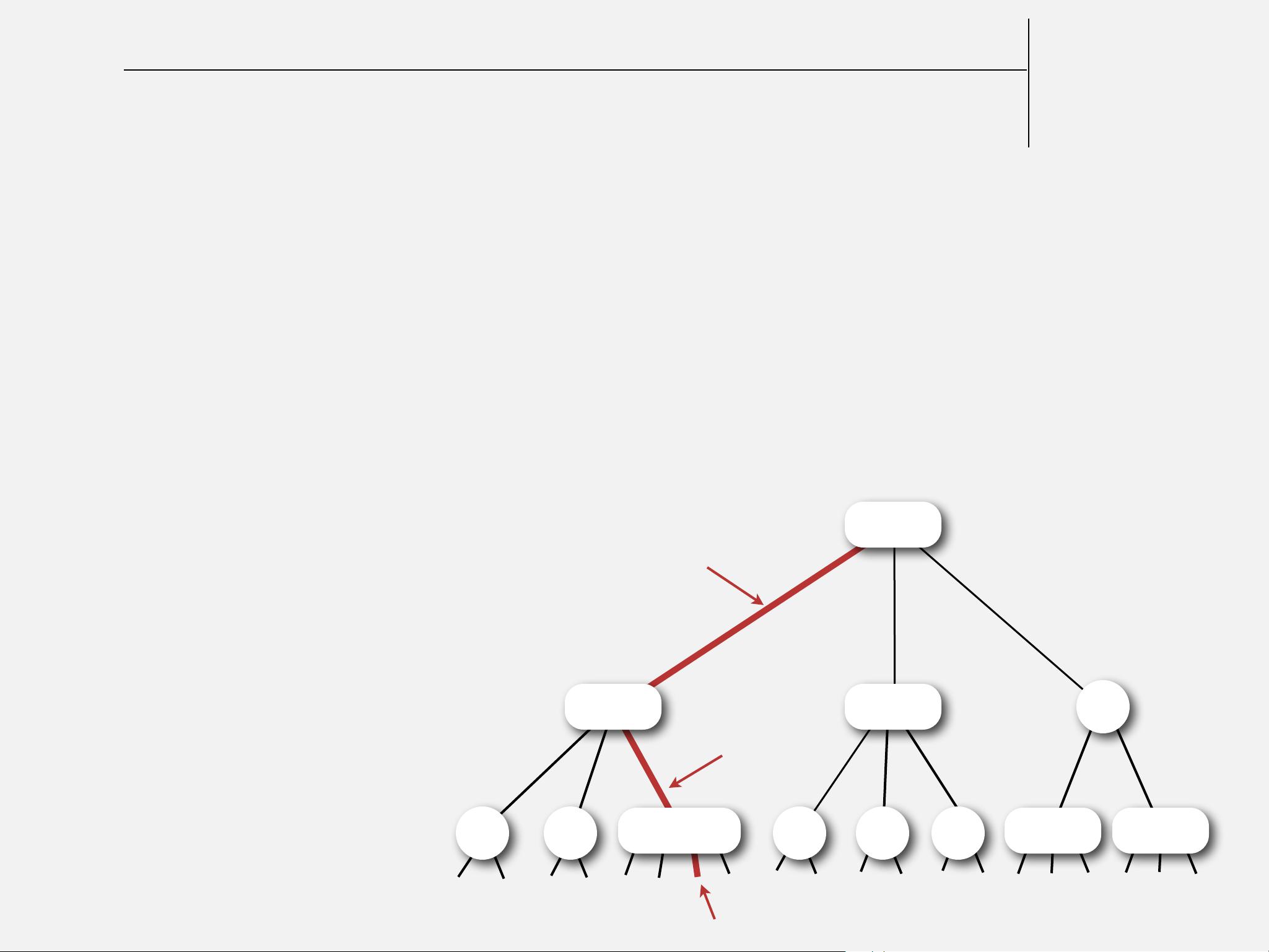 左倾红黑树是红黑树的一个变体，它的规则略有不同： - 左倾斜：所有的红色节点都倾向于向左链接，即不允许存在右红色链接。这简化了插入和删除操作的处理，尤其是在处理右旋情况时。 - 完全删除操作：资料指出左倾红黑树提供了完整的删除操作实现，这是红黑树实现中的一个重要部分，因为删除可能导致树的不平衡，需要通过旋转和重新着色来恢复平衡。 - 平衡4节点：资料提到回归平衡的4节点，这可能是指在某些情况下，节点可以拥有4个子节点，而不仅仅是2个，以更有效地处理插入和删除。 - 2-3树的联系：红黑树可以看作是2-3树的变种，2-3树是另一种自平衡树，其中节点可以有2个或3个子节点。左倾红黑树与2-3树的关系可能体现在它们的平衡策略上。 资料提供的Java代码和动态演示有助于直观地理解这些概念，并且对于学习和实践红黑树的算法非常有用。通过深入理解和掌握红黑树的原理，开发者可以在各种实际应用中，如数据库索引、图形渲染、编译器等，提高算法效率。