hierarchical data structure designed for a multiphase clustering
method. First, the database is scanned to build an initial in-
memory CF-tree which can be seen as a multi-level compres-
sion of the data that tries to preserve the inherent clustering
structure of the data. Second, an arbitrary clustering algorithm
can be used to cluster the leaf nodes of the CF-tree. Because
BIRCH is reasonably fast, it can be used as a more intelligent
alternative to data sampling in order to improve the scalability
of clustering algorithms.
3. Ordering The Database With Respect To
The Clustering Structure
3.1 Motivation
An important property of many real-data sets is that their intrin-
sic cluster structure cannot be characterized by global density
parameters. Very different local densities may be needed to re-
veal clusters in different regions of the data space. For example,
in the data set depicted in Figure 1, it is not possible to detect the
clusters A, B, C
1
, C
2
, and C
3
simultaneously using one global
density parameter. A global density-based decomposition
would consist only of the clusters A, B, and C, or C
1
, C
2
, and C
3
.
In the second case, the objects from A and B are noise.
The first alternative to
detect and analyze such
clustering structures is to
use a hierarchical cluster-
ing algorithm, for in-
stance the single-link
method. This alternative,
however, has two draw-
backs. First, in general it
suffers considerably
from the single-link ef-
fect, i.e. from the fact that
clusters which are con-
nected by a line of few points having a small inter-object dis-
tance are not separated. Second, the results produced by
hierarchical algorithms, i.e. the dendrograms, are hard to under-
stand or analyze for more than a few hundred objects.
The second alternative is to use a density-based partitioning al-
gorithm with different parameter settings. However, there are
an infinite number of possible parameter values. Even if we use
a very large number of different values - which requires a lot of
secondary memory to store the different cluster memberships
for each point - it is not obvious how to analyze the results and
we may still miss the interesting clustering levels.
The basic idea to overcome these problems is to run an algo-
rithm which produces a special order of the database with re-
spect to its density-based clustering structure containing the
information about every clustering level of the data set (up to a
“generating distance” ε), and is very easy to analyze.
3.2 Density-Based Clustering
The key idea of density-based clustering is that for each object
of a cluster the neighborhood of a given radius (ε) has to contain
at least a minimum number of objects (MinPts), i.e. the cardi-
nality of the neighborhood has to exceed a threshold. The for-
mal definitions for this notion of a clustering are shortly
introduced in the following. For a detailed presentation see
[EKSX 96].
Definition 1: (directly density-reachable)
Object p is directly density-reachable from object q wrt. ε
and MinPts in a set of objects D if
1) p ∈ N
ε
(q) (N
ε
(q) is the subset of D contained in the
ε-neighborhood of q.)
2) Card(N
ε
(q)) ≥ MinPts (Card(N) denotes the cardinal-
ity of the set N)
The condition Card(N
ε
(q)) ≥ MinPts is called the “core object
condition”. If this condition holds for an object p, then we call
p a “core object”. Only from core objects, other objects can be
directly density-reachable.
Definition 2: (density-reachable)
An object p is density-reachable from an object q wrt. ε
and MinPts in the set of objects D if there is a chain of ob-
jects p
1
, ..., p
n
, p
1
= q, p
n
= p such that p
i
∈D and p
i+1
is
directly density-reachable from p
i
wrt. ε and MinPts.
Density-reachability is the transitive hull of direct density-
reachability. This relation is not symmetric in general. Only
core objects can be mutually density-reachable.
Definition 3: (density-connected)
Object p is density-connected to object q wrt. ε and MinPts
in the set of objects D if there is an object o ∈D such that
both p and q are density-reachable from o wrt. ε and
MinPts in D.
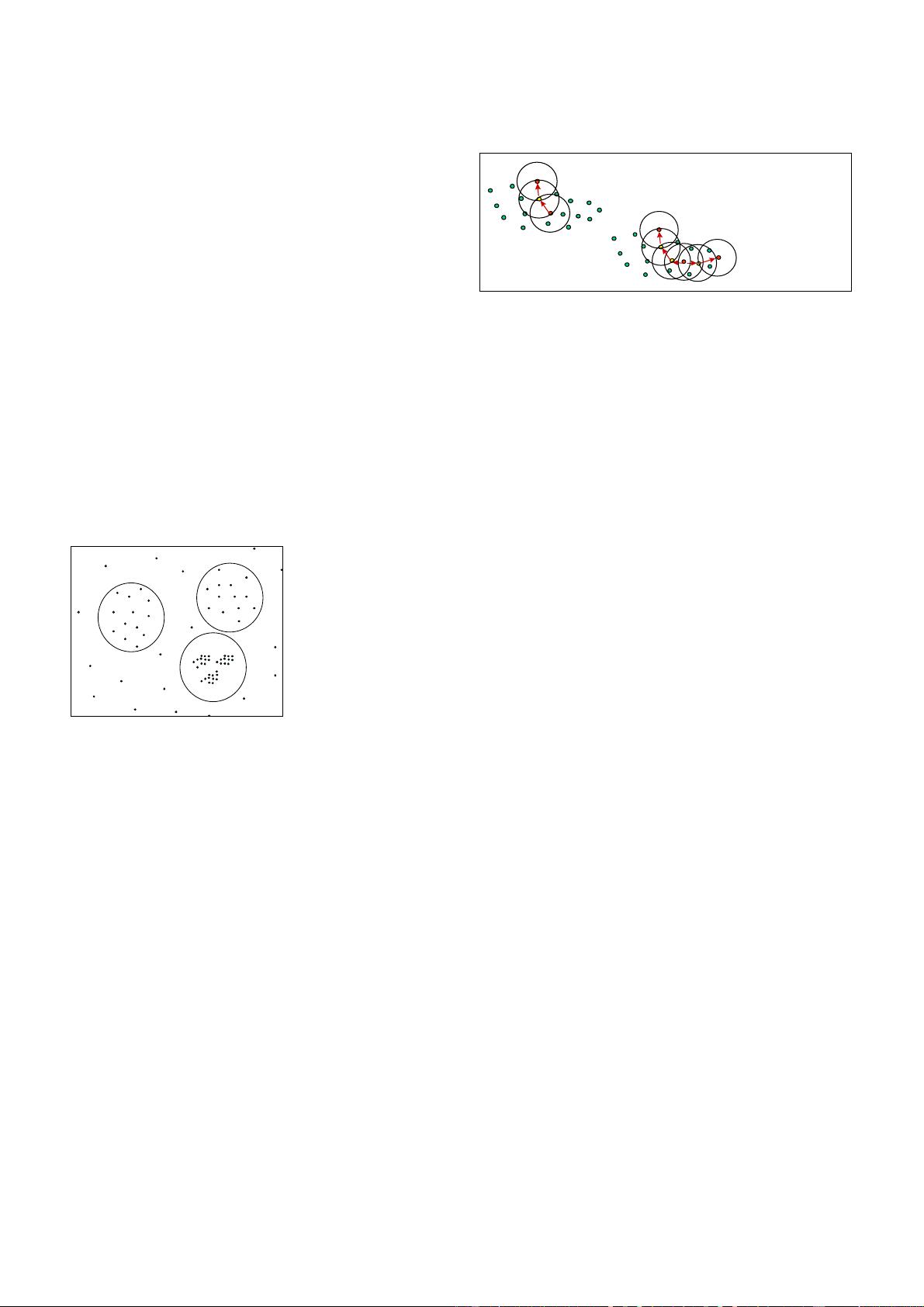
Density-connectivity is a symmetric relation. Figure 2 illus-
trates the definitions on a sample database of 2-dimensional
points from a vector space. Note that the above definitions only
require a distance measure and will also apply to data from a
metric space.
A density-based cluster is now defined as a set of density-con-
nected objects which is maximal wrt. density-reachability and
the noise is the set of objects not contained in any cluster.
Definition 4: (cluster and noise)
Let D be a set of objects. A cluster C wrt. ε and MinPts in
D is a non-empty subset of D satisfying the following con-
ditions:
1) Maximality: ∀p,q ∈D: if p ∈C and q is density-reach-
able from p wrt. ε and MinPts, then also q ∈C.
2) Connectivity: ∀p,q ∈ C: p is density-connected to q wrt.
ε and MinPts in D.
Every object not contained in any cluster is noise.
Note that a cluster contains not only core objects but also ob-
jects that do not satisfy the core object condition. These objects
Figure 1. Clusters wrt. different
density parameters
A
B
C
C
1
C
2
C
3
p
q
o
p
q
Figure 2. Density-reachability and connectivity
p density-reachable from q
q not density-reachable from p
p and q density-connected
to each other by o









