2 Type-2 fuzzy neural network
In this paper, we consider the general multi-input–single-
output system, whose input variables are supposed to be
x ¼ðx
1
; ...; x
p
Þ2X
1
X
2
X
p
:
By assigning the jth input variable N
j
T2FSs, we can
obtain the following fuzzy rule base with
Q
p
j¼1
N
j
fuzzy
rules:
Ruleði
1
; i
2
; ...; i
p
Þ: x
1
¼
e
A
i
1
1
; x
2
¼
e
A
i
2
2
; ...; x
p
¼
e
A
i
p
p
!
y
o
ðxÞ¼½w
i
1
i
2
...i
p
; w
i
1
i
2
...i
p
; where i
j
¼ 1; 2...; N
j
; ½w
i
1
i
2
...i
p
;
w
i
1
i
2
...i
p
s are the interval weights,
e
A
i
j
j
s are T2FSs for the jth
input variable.
Corresponding to this type-2 fuzzy rule base, the
structure of the T2FNN can be constructed as shown in
Fig. 1. The T2FNN works as follows in each layer.
Layer 1-fuzzification layer: There are p nodes in this
layer. For analysis simplicity, singleton fuzzifier is adopted
in this layer.
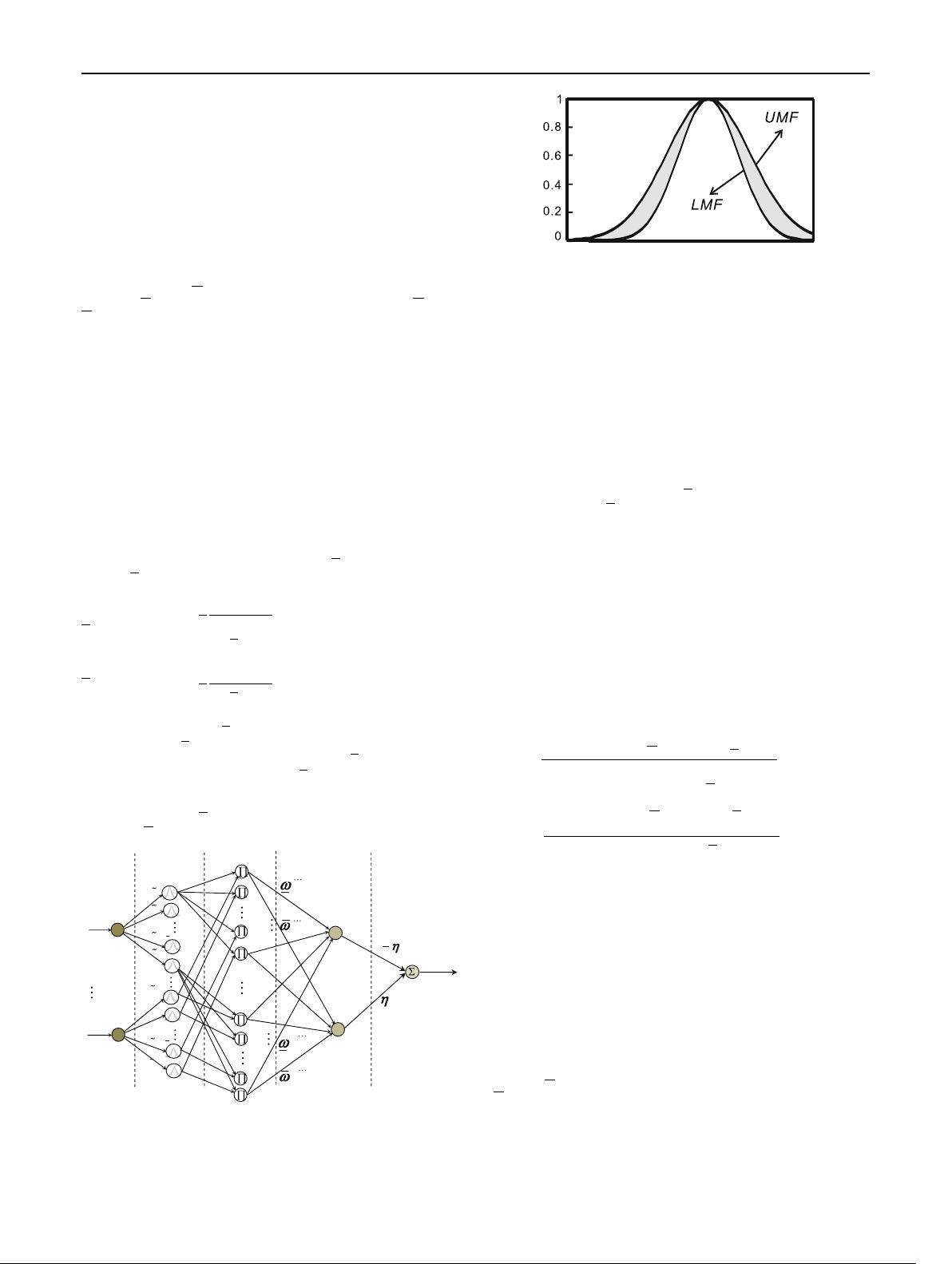
Layer 2-type-2 MF layer: In this layer, each node per-
forms a T2FS, and there are
P
j=1
p
N
j
nodes in this layer.
With the choice of Gaussian T2FS (see Fig. 2), the T2FS
e
A
i
j
j
can be represented as an interval bound by its lower MF
(LMF)
l
e
A
i
j
j
ðx
j
Þ and upper MF (UMF) l
e
A
i
j
j
ðx
j
Þ :
l
e
A
i
j
j
ðx
j
Þ¼exp
1
2
ðx
j
c
i
j
j
Þ
2
ðd
i
j
j
Þ
2
2
4
3
5
; ð1Þ
l
e
A
i
j
j
ðx
j
Þ¼exp
1
2
ðx
j
c
i
j
j
Þ
2
ðd
i
j
j
Þ
2
2
4
3
5
; ð2Þ
where c
i
j
j
and ½ðd
i
j
j
Þ
2
; ðd
i
j
j
Þ
2
are, respectively, the center and
uncertain widths of
e
A
i
j
j
; and 0\ðd
i
j
j
Þ
2
ðd
i
j
j
Þ
2
:
The output of each node can be represented as an
interval
l
e
A
i
j
j
ðx
j
Þ; l
e
A
i
j
j
ðx
j
Þ
:
Layer 3- Rule Layer: Each node in this layer represents
one fuzzy logic rule and performs precondition matching of
a rule. So, there are
Q
p
j¼1
N
j
nodes in this layer. The output
of a rule node represents the firing strength of this fuzzy
rule. For the node ði
1
; i
2
; ...; i
p
Þ corresponding to Rule
ði
1
; i
2
; ...; i
p
Þ, its firing strength is calculated by the prod-
uct operation as follows:
F
i
1
i
2
i
p
ðxÞ¼
Y
p
j¼1
l
e
A
i
j
j
ðx
j
Þ;
Y
p
j¼1
l
e
A
i
j
j
ðx
j
Þ
"#
: ð3Þ
Layer 4-type-reduction layer: This layer is used to
achieve the type-reduction. In this layer, different type-
reducers may give different results. For simplicity, we
adopt Begian–Melek–Mendel (BMM) method proposed in
[12] to realize the type-reduction. With this type-reduction
method, the input–output mappings of T2FNNs have
closed-form expressions, which makes it convenient to do
theoretical analysis. Using the BMM method, the output of
the two nodes in the fourth layer can be computed as:
y
l
ðxÞ¼
P
N
1
i
1
¼1
P
N
p
i
p
¼1
w
i
1
i
2
i
p
Q
p
j¼1
l
e
A
i
j
j
ðx
j
Þ
P
N
1
i
1
¼1
P
N
p
i
p
¼1
Q
p
j¼1
l
e
A
i
j
j
ðx
j
Þ
; ð4Þ
y
u
ðxÞ¼
P
N
1
i
1
¼1
P
N
p
i
p
¼1
w
i
1
i
2
i
p
Q
p
j¼1
l
e
A
i
j
j
ðx
j
Þ
P
N
1
i
1
¼1
P
N
p
i
p
¼1
Q
p
j¼1
l
e
A
i
j
j
ðx
j
Þ
: ð5Þ
Layer 5-output layer: This layer performs the
defuzzification. Here, we use the linear combination of
y
l
ðxÞ and y
u
ðxÞ to generate the crisp output, that is,
y
o
ðxÞ¼ð1 gÞy
l
ðxÞþgy
u
ðxÞ; ð6Þ
where g is the defuzzification coefficient, and 0 B g B 1.
A T2FNN can be seen as a multivariable function y
o
ðxÞ:
When all sources of uncertainty disappear, the T2FSs
e
A
i
j
j
s
in Layer 2 becomes T1FSs A
i
j
j
s, and the interval weights
½
w
i
1
i
2
...i
p
; w
i
1
i
2
...i
p
s between Layer 3 and Layer 4 becomes
crisp weights w
i
1
i
2
...i
p
s. Hence, the T2FNN turns to a
T1FNN.
1
1
2
1
1
1
1
N
A
1
1
N
()
l
yx
11
Layer 1 Layer 2 Layer 3 Layer 4 Layer 5
1
p
A
1
p
N
p
A
p
N
p
1
x
p
x
1
NN
()
u
yx
1
()
o
yx
1 p
NN
11
Fig. 1 Structure of type-2 fuzzy neural network
Fig. 2 A Gaussian T2FS with uncertain widths
Neural Comput & Applic (2013) 23:1987–1998 1989
123









