基于Shifted Legendre多项式的分数阶微分方程数值解法

"分数阶微分方程在众多科学领域中有着广泛的应用，如工程、人口学、医学、流体力学以及化学和物理学的分支。分数微分方程（FDEs）被用来精确地描述这些领域的复杂动态过程。Shifted Legendre操作矩阵（LOM）方法是一种解决FDEs的常用技术，本文作者提出了一种基于移位勒让德多项式的数值解法，用于处理分数阶微分方程的初值和边值问题。通过构建分数阶运算矩阵，将Caputo导数形式的分数阶导数转化为矩阵乘积的形式，从而将原问题转化为线性方程组。这种方法被证明是高效且适用的，通过数值实例与解析解的比较，进一步验证了其有效性。" 在这篇发表于《Advances in Pure Mathematics》2018年8月的文章中，作者A.M.Kawala探讨了分数阶微分方程的数值解法。分数阶微积分因其对非局部性和历史效应的捕捉能力，在多个学科中成为重要的数学工具。Caputo导数是分数阶导数的一种常见定义，它在实际应用中尤为实用，因为它消除了初始条件的奇异性。 文章的核心是Shifted Legendre多项式为基础的数值方法。移位勒让德多项式是一种在数值分析中常用的正交多项式，它们在解决微分方程时能提供高精度的近似。作者构造了一个分数阶的勒让德运算矩阵，该矩阵包含了Caputo导数的定义，使得分数阶微分方程可以通过矩阵运算来处理。通过这种方式，复杂的分数阶初值和边值问题被转换成简单的线性代数问题，即求解一组线性方程组。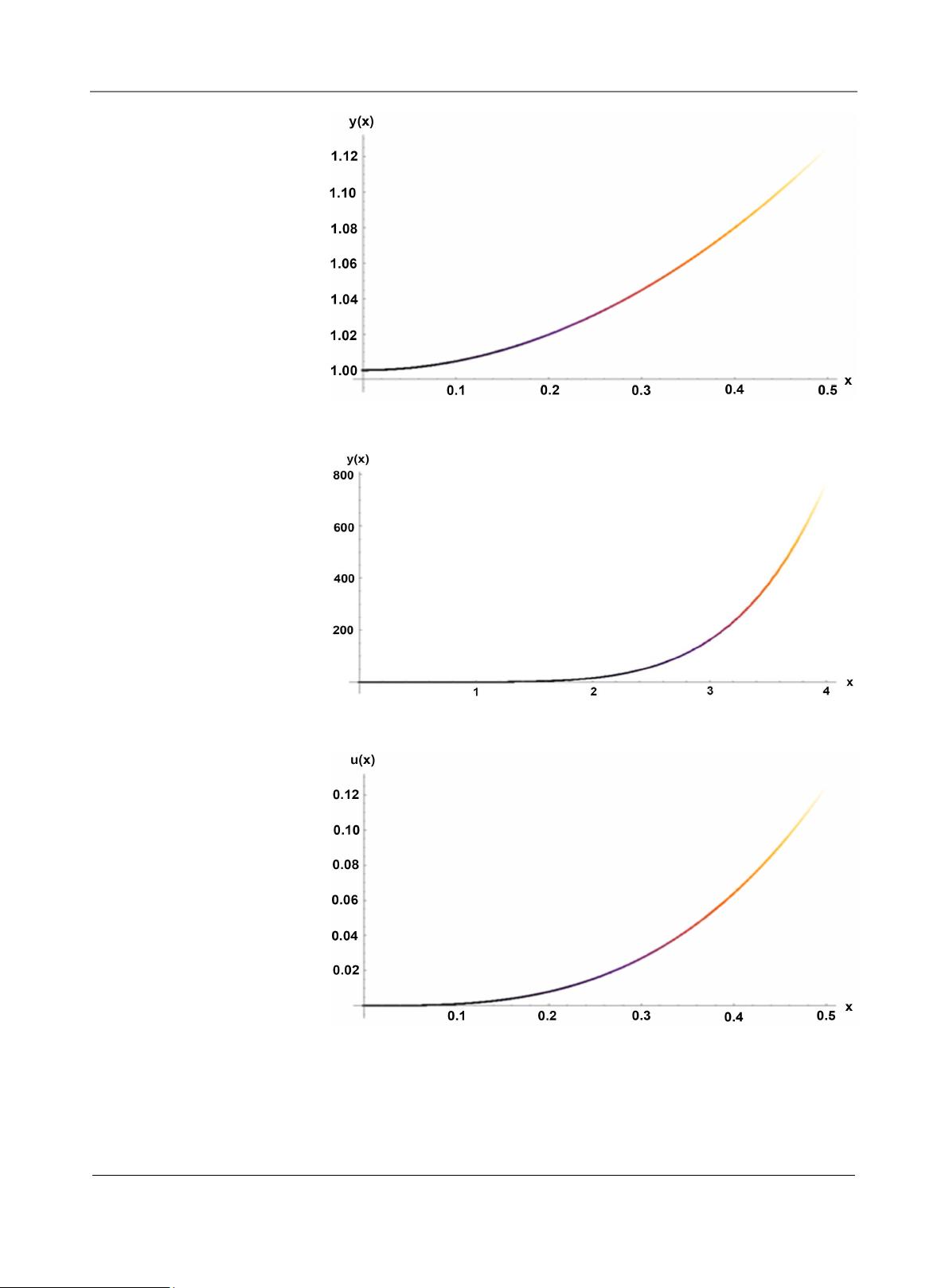 作者展示了这种方法的实用性，通过数值实验比较了得到的结果与解析解，证明了所提出的数值方法具有高度的准确性和效率。这为解决实际问题中遇到的分数阶微分方程提供了新的计算策略，尤其对于那些传统方法难以处理的问题，这种方法可能提供更优的解决方案。 这篇论文为理解和应用分数阶微分方程的数值解法提供了有价值的贡献，特别是在利用移位勒让德多项式和Caputo导数的情况下，它为科研人员和工程师提供了一种有效的数值工具。