提升小波变换解析：杨老师信息科学讲义

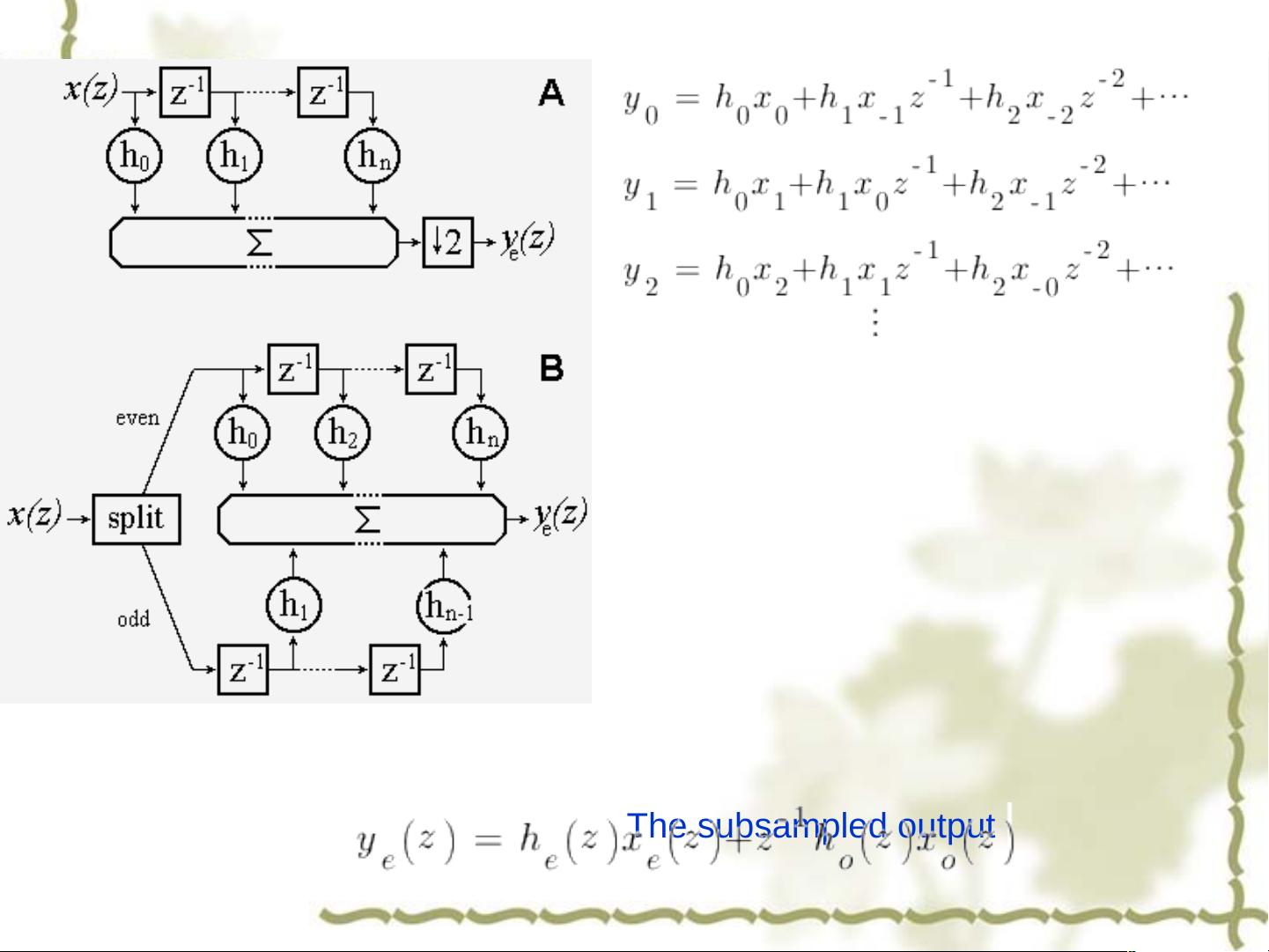
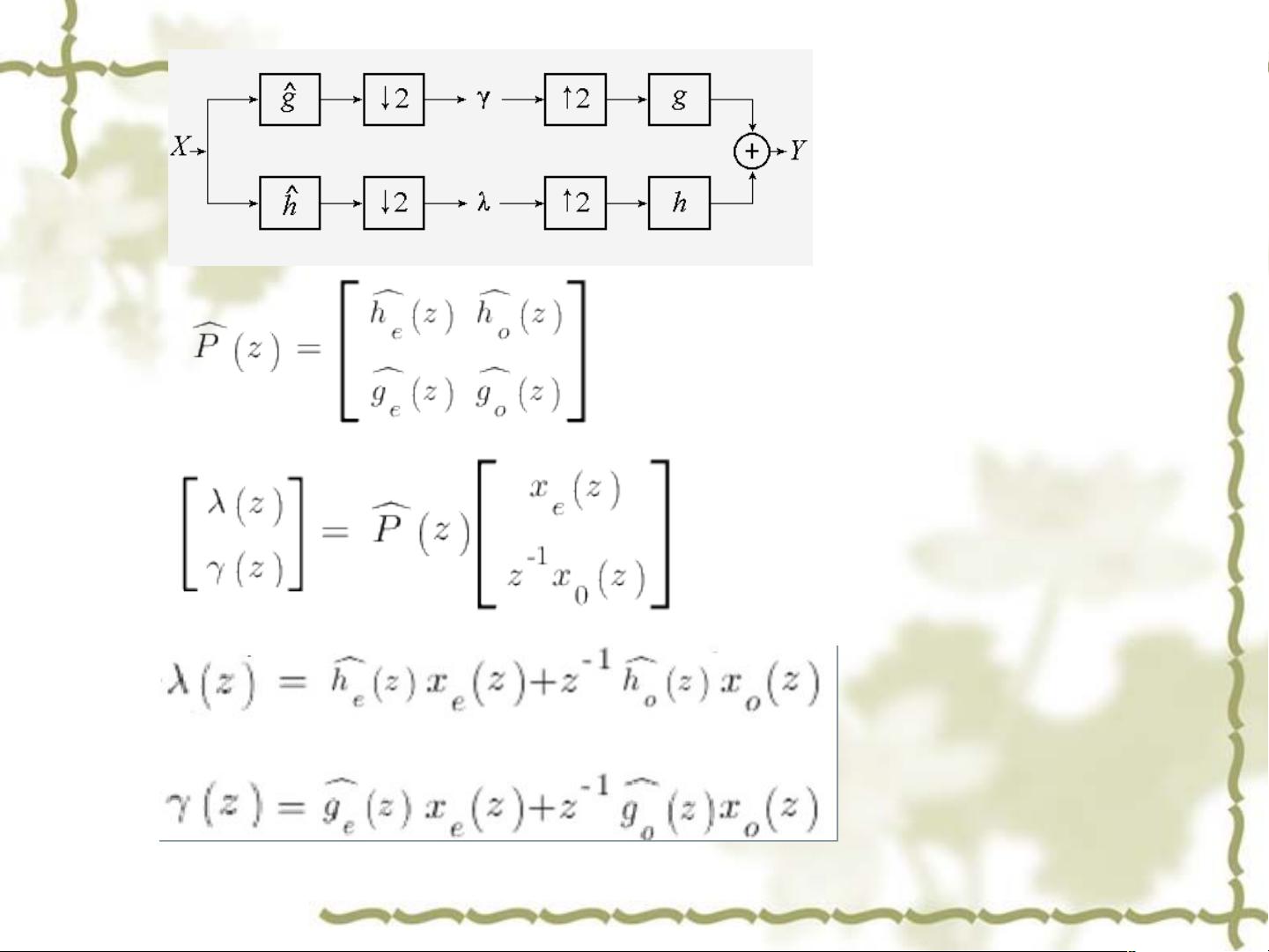
"提升小波变换讲义 - 杨明强 - 山东大学信息科学与工程学院" 在小波分析领域，提升小波变换（Lifting Wavelet Transform）是一种高效且实用的算法，由杨明强教授在山东大学信息科学与工程学院的课程中讲解。与传统的第一代小波变换相比，提升小波变换提供了更为直观和计算效率更高的方法，它不再依赖傅里叶变换（即不涉及卷积操作），并且在计算整数小波变换时表现出优越性。 9.1 从经典小波变换到提升小波变换 提升小波变换为理解小波变换提供了一种新的途径，它避免了经典小波变换中对傅里叶变换的依赖。这一变换方式更简洁、执行效率更高，比传统的第一代小波变换速度快一倍。更重要的是，提升小波变换使得计算整数小波变换变得容易，并通过原地计算（In-place computation）显著减少了内存需求，即用存储输入数据的内存直接覆盖小波系数，降低了存储开销。 提升过程（Lifting） 任何有限滤波器长度的离散小波变换或双带子带滤波器都可以分解为一系列提升步骤。这个转换完全在空间域内进行，因此傅里叶分析在这个过程中不再是必需的。提升步骤使得小波变换的计算更加直观，不再需要复杂频域分析，简化了整个过程。 小波变换或子带编码通常使用滤波器组来实现。分析滤波器和合成滤波器（如h(z)和g(z)）用于分解和重构信号。提升小波变换则通过一系列简单的操作（例如预测和更新步骤）来实现这种分解，这些操作都在原始数据上直接进行，从而提高了效率。 提升小波变换的优势： 1. 计算效率高：提升小波变换的算法结构简单，减少了计算量，特别是在处理大规模数据时。 2. 整数特性：提升算法非常适合进行整数小波变换，这对于图像处理和数据压缩等应用至关重要。 3. 内存优化：通过原地计算，提升小波变换可以节省大量内存，尤其在资源有限的环境中。 4. 灵活性：提升框架允许设计者灵活地调整滤波器参数，以优化特定应用的性能。 总结来说，提升小波变换是小波理论的一个重要进展，它提供了一种更高效、更易于理解和实现的方法，广泛应用于信号处理、图像压缩、数据压缩以及噪声去除等多个领域。杨明强教授的讲义深入浅出地介绍了这一技术，对于学习和掌握提升小波变换具有很高的价值。