三角波信号的匹配滤波器分析与SNR计算（王景博作业）

在信号检测与估计的第二章作业中，学生王景博针对输入信号为三角波的问题进行了深入分析。该作业要求确定白噪声背景下匹配滤波器（Matched Filter, MF）的相关参数。匹配滤波器是一种特殊的滤波器设计，用于最大化信号检测性能，特别是在高斯白噪声环境下。 首先，匹配滤波器的冲激响应被设计为输入三角波信号的翻转共轭，以适应白噪声条件。对于因果系统，其冲激响应可以表示为： h[n] = K * (sgn(x[n]) * u[n - τ]) 这里，K是常数，通常取1，τ是时间延迟，确保信号的因果性。在数字系统中，由于存储能力，非因果系统可以实现，但可能牺牲实时性。三角波信号为矩形信号（门信号）的线性卷积，因此可以通过门函数的傅里叶变换来计算频域传递函数： H(f) = F{h[n]} = K * X(f) / |X(f)| X(f)是三角波信号的频域表示，而|X(f)|是其幅度谱，|X(f)|^2给出了门函数的频域表示。 输出的最大信噪比（Signal-to-Noise Ratio, SNR）由MF理论给出，公式为： SNR_max = 10 * log10[E / (P_n * T)] 其中E是输入信号的能量，P_n是输入白噪声的功率谱密度。由于白噪声是随机的，需要通过大量样本观测或自相关函数计算来估计其功率谱密度。在本题中，假设功率谱密度已知，不进行具体计算。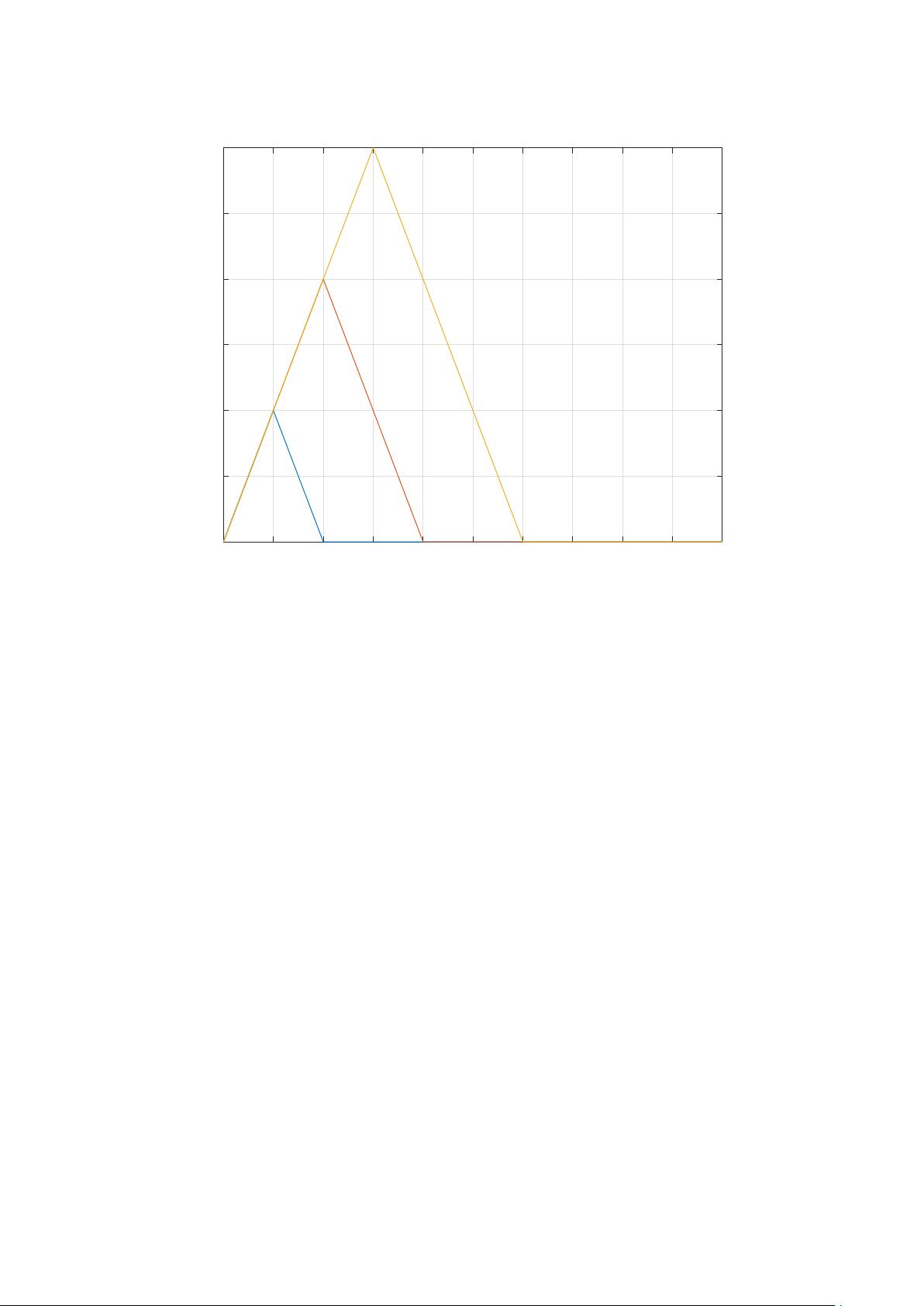 在无噪声情况下，输出信号为两个三角波的线性卷积，而在有噪声时，输出信号为： y[n] = x[n] * h[n] + n[n] 其中n[n]是输入白噪声信号。有噪声输出信号的表达式较为复杂，因为它包含了噪声成分，无法给出精确的解析形式。 当输入信号的SNR设为-20dB时，图1展示了输入信号与噪声的关系，显示了信号被显著淹没在噪声中的情况。图2则展示了匹配滤波器的冲激响应以及幅频响应，后者体现了匹配滤波器仅与输入信号相关的特点，与输入噪声无关。 这个作业涉及到了匹配滤波器的基本原理，包括信号处理技术、频域分析，以及噪声环境下的信噪比优化，是信号检测理论在实际问题中的应用实例。