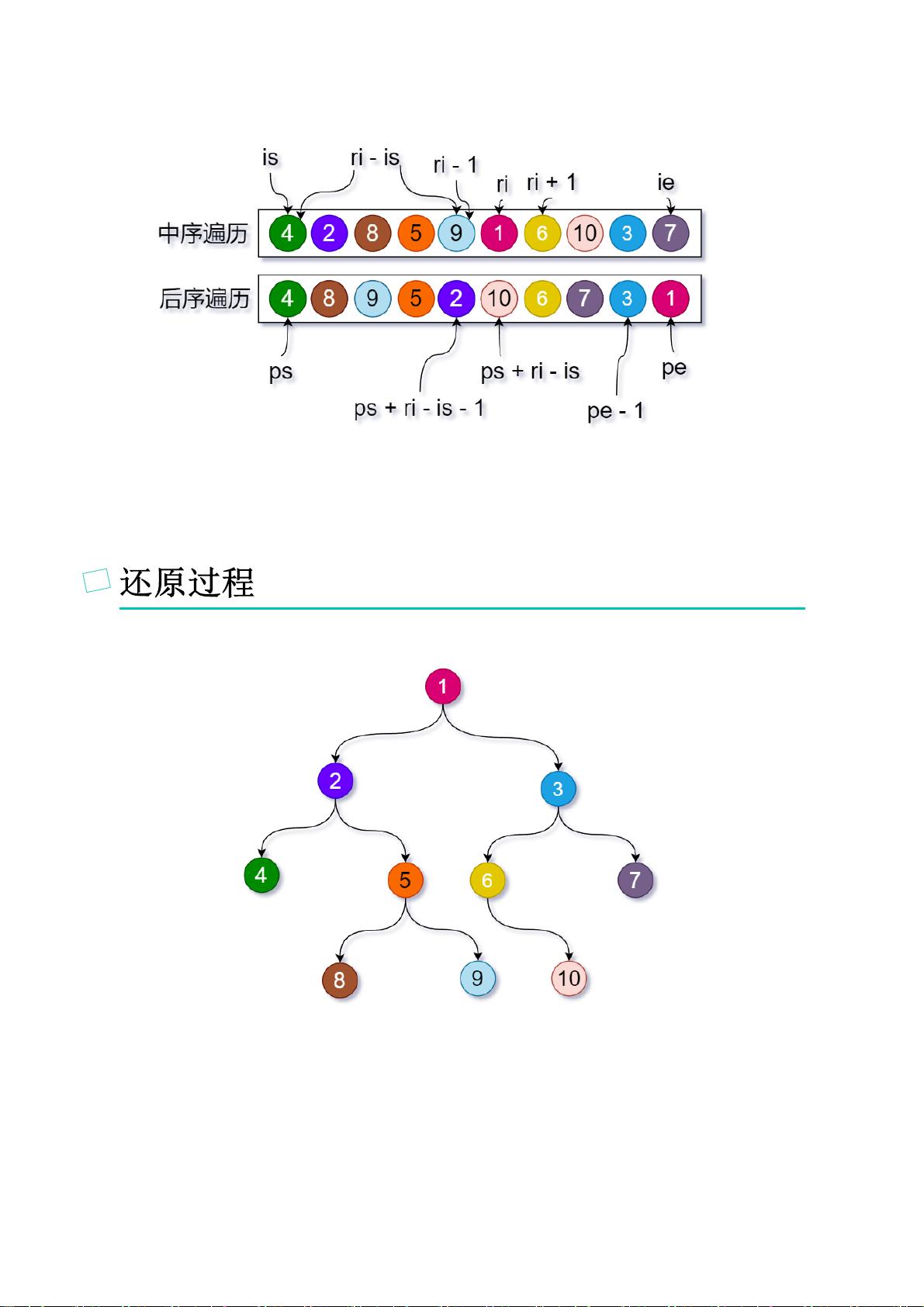
根据中序与后序遍历构建二叉树

"这篇资料主要讨论了如何通过中序遍历(inorder)和后序遍历(postorder)的结果来重建二叉树。" 在计算机科学中，二叉树的遍历是理解和操作二叉树数据结构的关键技术。二叉树有三种主要的遍历方式：前序遍历、中序遍历和后序遍历。本资料重点介绍了如何利用中序遍历和后序遍历的序列来构建原二叉树。 中序遍历的特点是从左到右依次访问左子树、根节点和右子树，而后序遍历则是先遍历左子树和右子树，最后访问根节点。这两个遍历序列提供了重构二叉树的重要线索。 例如，给定如下的中序遍历`inorder = [9, 3, 15, 20, 7]`和后序遍历`postorder = [9, 15, 7, 20, 3]`，可以重建以下二叉树： ``` 3 / \ 9 20 / \\ 15 7 ``` 重建过程分为以下几个步骤： 1. **找到根节点**：后序遍历序列的最后一个元素是根节点。在上述例子中，根节点是3。 2. **确定中序遍历中的根节点位置**：在中序遍历序列中找到根节点3，其索引为1（从0开始计数）。 3. **划分左右子树**：根据根节点在中序遍历序列中的位置，将序列划分为左子树（索引0到0）和右子树（索引2到4）。 4. **递归构建子树**：分别对左子树和右子树进行相同的操作，直到所有节点都处理完毕。 在这个过程中，需要记录一些关键信息，例如： - `memo`：一个哈希表，存储中序遍历序列中每个元素对应的索引。 - `intri`：根节点在中序遍历数组中的索引。 - `is` 和 `ie`：分别表示中序遍历数组的起始和结束索引。 - `ps` 和 `pe`：表示后序遍历数组的起始和结束索引。 在找到根节点后，根据根节点的索引计算左右子树在中序和后序遍历序列中的边界，然后递归地构造左子树和右子树。 以下是基于这些概念的Java实现代码片段，用于重建二叉树： ```java class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } public TreeNode buildTree(int[] inorder, int[] postorder) { // 实现细节... } ``` 实际的`buildTree`方法会包含查找根节点、划分子树和递归构建子树的逻辑。这个过程涉及到递归和数组操作，对于理解二叉树和遍历非常重要。 理解中序和后序遍历的关系，并能够据此重建二叉树，是解决这类问题的关键。在编程面试和算法竞赛中，这类问题经常出现，因此熟练掌握这种方法对提升编程技能非常有益。