层次分析法详解：解决复杂决策问题的关键工具

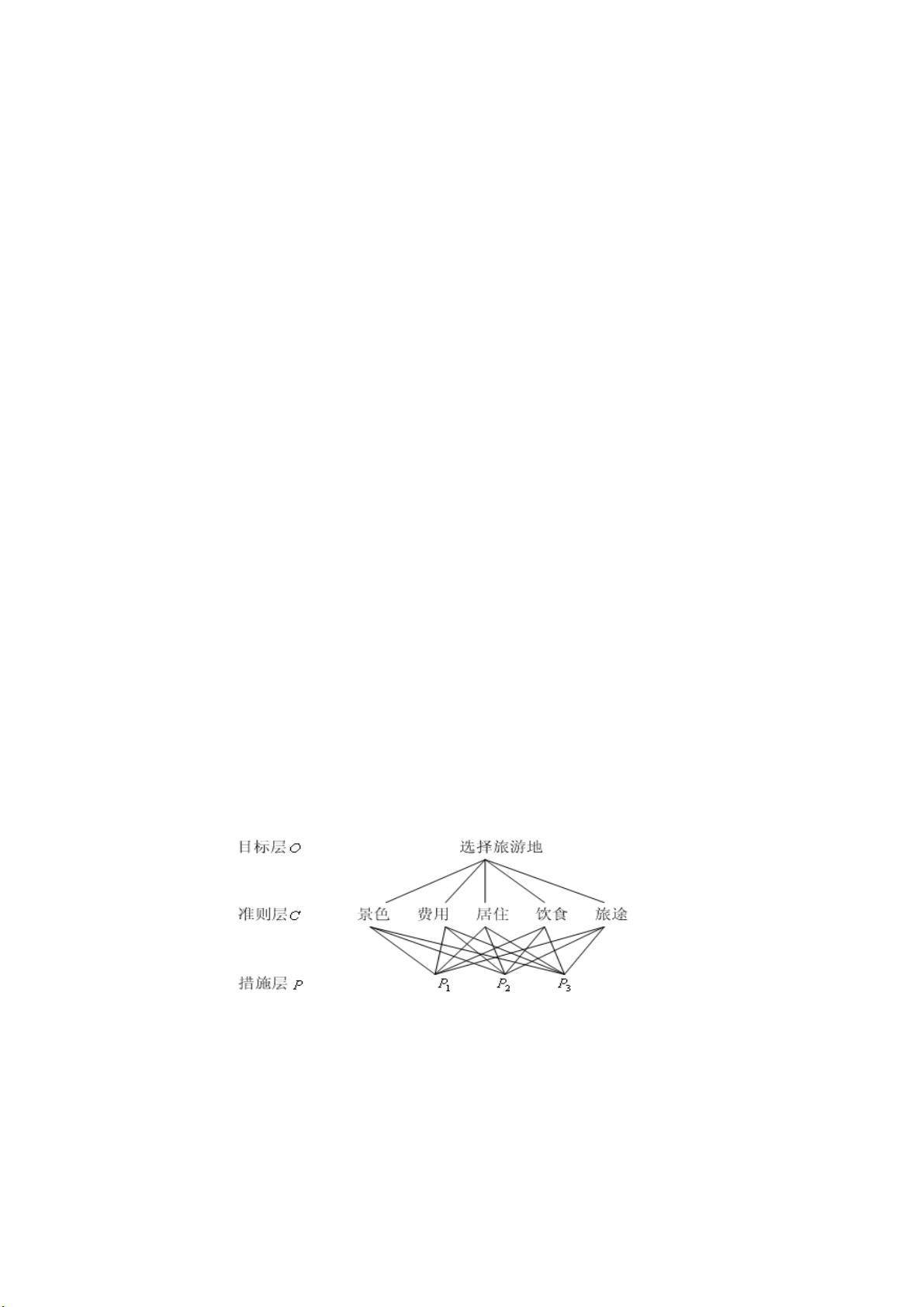
层次分析法（Analytic Hierarchy Process, AHP）是一种多准则决策工具，用于解决复杂且模糊的问题。它由美国运筹学家T.L.Saaty在上世纪70年代提出，特别适合于难以进行定量分析的情况。AHP通过构建递阶层次结构模型，将复杂问题分解成各个层次，包括目标层、准则层和措施层，以清晰地展现要素间的相互关系。 1. **层次结构的构建**: - 建立层次结构是AHP的核心步骤。首先，将问题分解成一个有层次的结构，比如在例1中，选择最佳旅游地点时，可能会考虑风景、费用、住宿、餐饮和旅途条件等准则，这些构成了准则层。 - 目标层通常代表最终决策的目标或理想结果，例如寻找最佳旅游地点；准则层则包含影响目标实现的关键因素；措施层是可供选择的具体行动方案。 - 递阶层次的层数可根据问题复杂度调整，但准则层中每个准则的重要性可能不同，需要用判断矩阵来量化比较。 2. **判断矩阵的构造**: - 判断矩阵用于表示决策者对各准则相对重要性的主观评估。矩阵的行代表上一层的准则，列代表下一层的元素，每个单元格是两个元素间相对重要性的评分，通常用1到9的标度表示，其中1表示同等重要，9表示非常不重要。 - 一致性检验是关键步骤，通过计算判断矩阵的特征根和一致性比率，确保决策者的权重分配是一致的，避免偏见影响决策结果。 3. **排序与检验**: - 分别进行层次单排序和层次总排序。层次单排序是指对每个层次内的元素进行排序，确定其相对优先级。层次总排序则是将所有层次的结果综合起来，得出整个问题的最终排序。 - 一致性检验是为了确保决策过程中没有显著的偏差，若一致性比率过高（一般小于0.1），可能需要重新调整判断矩阵，直到达到满意的水平。 4. **实例说明**: - 例1中的旅游目的地选择问题通过构建层次结构，将决策问题分解为目标（找到最佳地点）、准则（景色、费用等）和候选地点，然后用判断矩阵表达决策者对各项准则的相对重视程度，最后进行排序和一致性检验。 层次分析法通过层次化的思维框架和定量与定性的结合，帮助决策者系统地分析和权衡复杂的决策问题，提高决策的准确性和可靠性。