PID参数详解与整定实战：提升控制系统性能

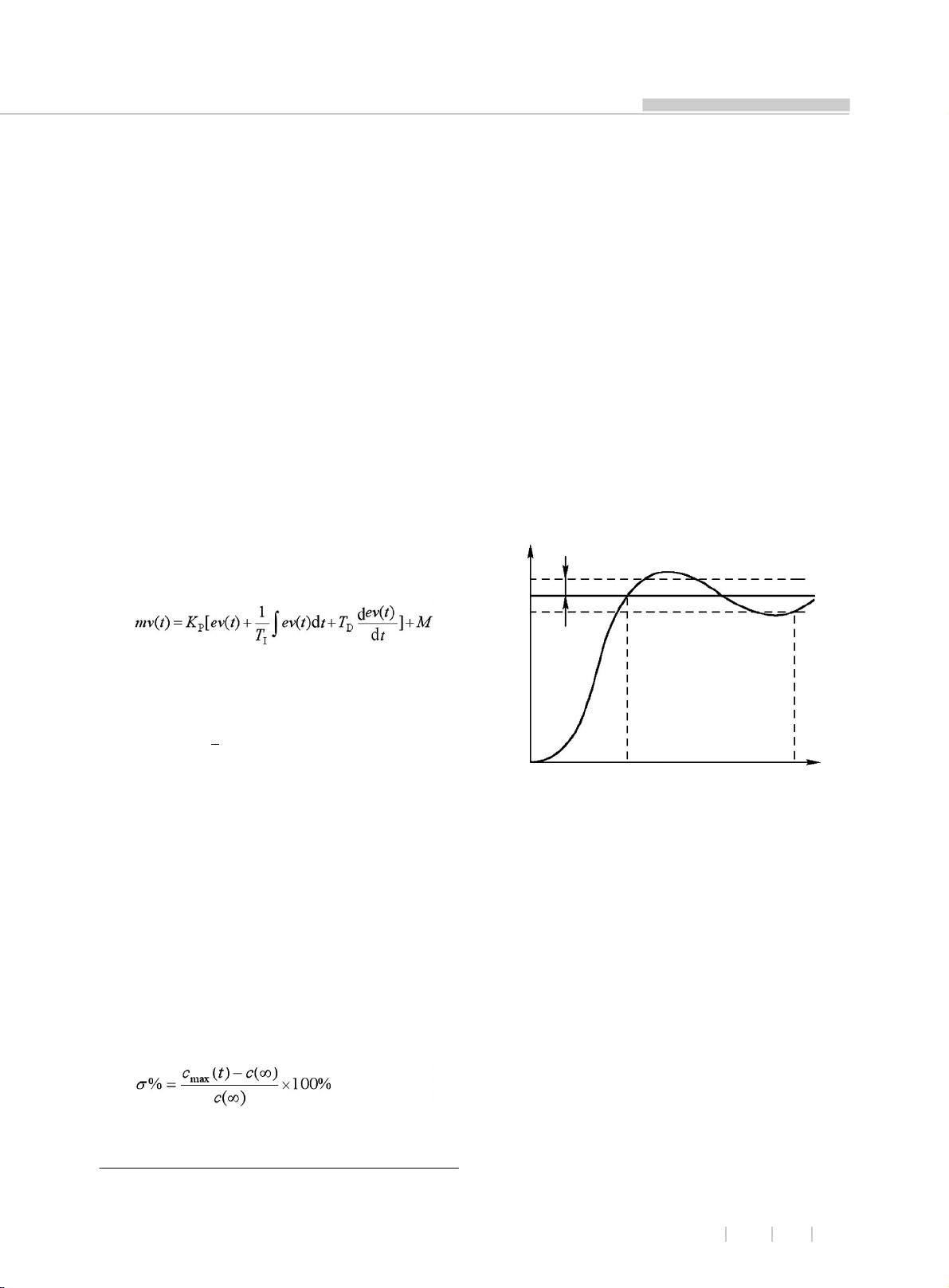
PID参数是Proportional-Integral-Derivative控制器的核心组成部分，它们在模拟量控制系统中发挥着至关重要的作用。PID控制器的数学表达式由比例(P)、积分(I)和微分(D)三部分组成，其输出公式为： 1. 比例作用：控制器的输出mv(t)与误差ev(t)成正比，即mv(t) = KP * ev(t)，其中KP是比例系数，决定着对当前误差的快速反应程度。 2. 积分作用：积分部分使得控制器能够消除系统误差积累，通过TI（积分时间）影响输出，当积分达到M（积分部分的初始值）时，会持续调整直到误差消失。 3. 微分作用：微分部分通过TD（微分时间）测量误差的变化率，帮助预测未来趋势，提前修正错误，提高控制精度。 闭环控制系统的关键性能指标包括： - 阶跃响应：阶跃输入下，系统的动态响应通常被描绘为阶跃响应曲线，它展示了系统从初始状态到稳定状态的过程。调节时间ts指的是误差进入稳态误差带（通常为±5%或±2%）所需的时间，这个时间标志着过渡过程的结束。 - 超调量：当系统响应超过稳态值C_max(t)时，超调量（即C_max(t) - c(∞)）衡量了系统响应的振荡程度，反映了系统稳定性的一个侧面。 整定PID参数的方法通常涉及以下几个步骤： 1. 经验法：基于工程师的经验和对系统的理解，设置初始参数值，然后通过实际运行和观察，逐步调整。 2. Ziegler-Nichols法：一种常用的整定方法，通过确定比例带PB、积分时间TI和微分时间TD的初始值，然后通过递增比例带，测量系统的响应，直至找到稳定的平衡点。 3. 自适应控制：利用在线学习算法，根据实时的系统数据调整参数，自动适应环境变化。 4. 最优控制理论：更高级的方法如模型预测控制(MPC)或自校正PID（自整定PID），通过优化算法寻求参数的最佳组合，以实现最小化误差和响应时间的目标。 本文通过仿真实验验证了PID参数整定方法的有效性，强调了参数选择对控制系统性能的影响，并提供了实用的参数调整策略。了解并合理设置PID参数对于实现高效、稳定的自动化控制至关重要，尤其是在伺服及PLC控制系统中，PID参数的精确调整直接影响到系统的响应速度、精度和稳定性。