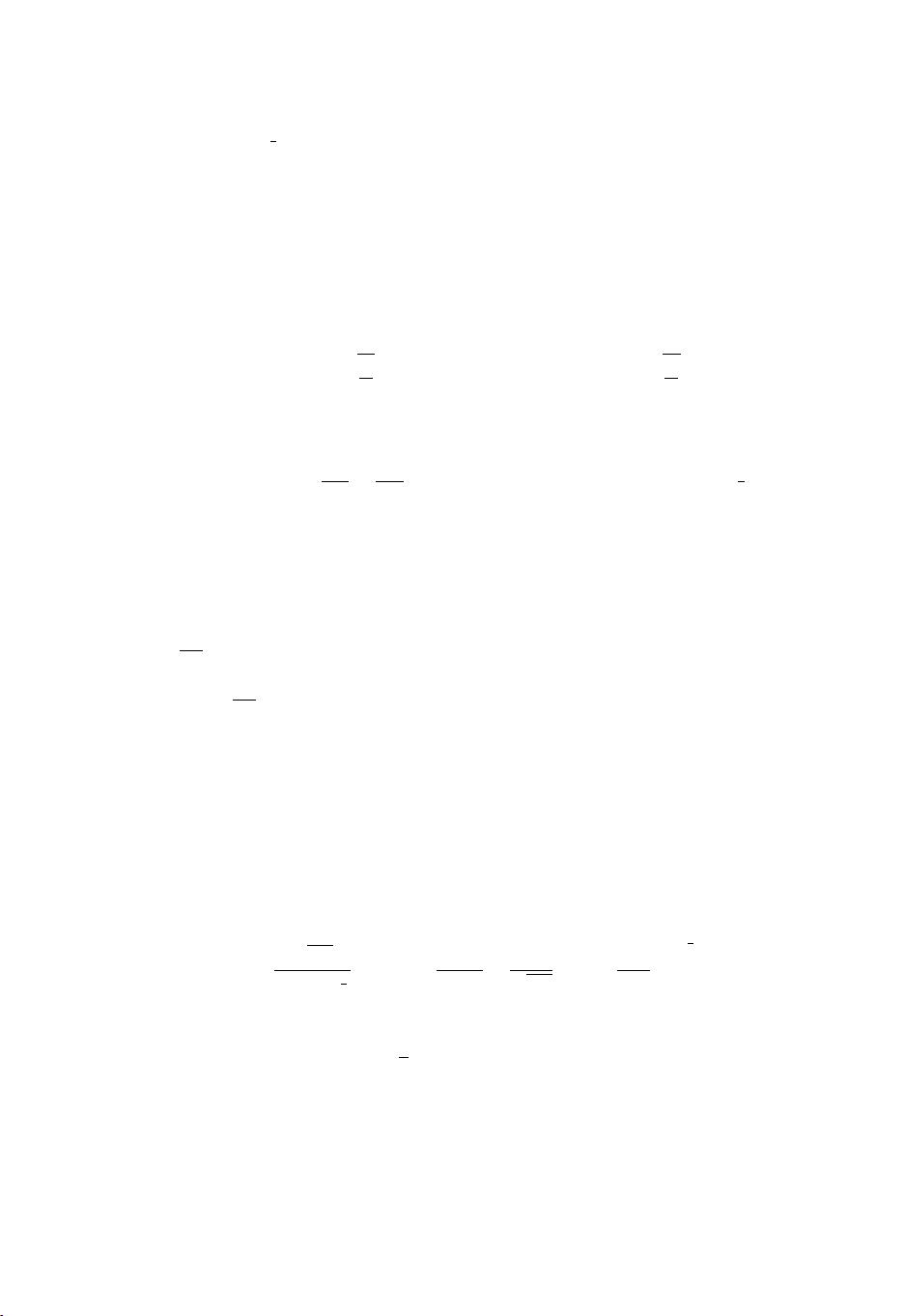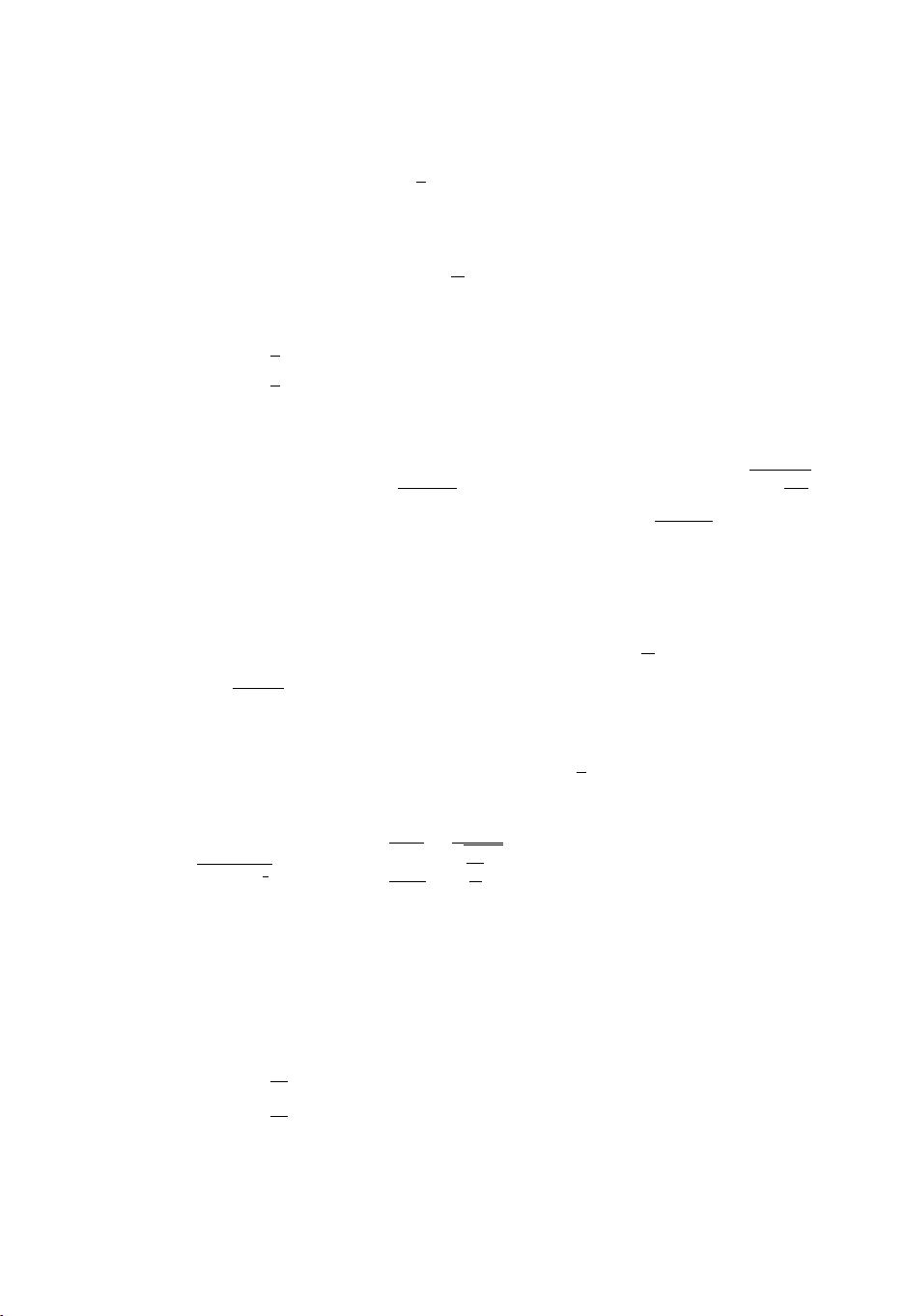量子线与拓扑超导体结的相图：费米子模式与非平凡不动点

172 浏览量更新于2024-07-16 收藏 747KB PDF 举报

"这篇文章探讨了在具有边界相互作用的系统中如何使用实际费米子模式（包括马约拉纳模和克莱因因子）扩展杂质熵。研究集中在N个相互作用量子线与拓扑超导体的结以及三个无旋转相互作用量子线的Y结上。文章揭示了N=2拓扑超导体结与Y结之间的显著对应关系，并讨论了如何通过调整系统参数来实现这一对应，同时展示Y结相图中新型‘平面’有限耦合不动点的出现。" 本文是核物理B期刊944期的一篇开放获取文章，由Domenico Giuliano、Ian Affleck等人撰写。作者们深入研究了相互作用量子线与拓扑超导体接头的相图，特别是杂质熵在其中的作用。杂质熵是描述系统中杂质影响的量化指标，而马约拉纳模和克莱因因子则是理解这些边界相互作用的关键工具。马约拉纳模，作为零模实际费米子算子，是量子线路和拓扑超导体领域的重要概念，它们具有自身反粒子的特性，对于量子计算有潜在的应用价值。克莱因因子则帮助处理系统中的对称性问题，特别是在多通道或多模式系统中。作者们通过具体应用他们的方法，分析了N个量子线与一个拓扑超导体形成的结。这种结构允许研究者探索不同数量的量子线与拓扑超导体相互作用时的相变和稳定性。他们特别指出，当N=2时，拓扑超导体结与Y结之间存在一种对应关系，这为理解和控制系统的相位提供了新的视角。此外，研究还关注了Y结的相图，这是一个三量子线交叉的结构，其中每个线都可能携带不同的量子态。在特定的系统参数下，Y结的相图揭示了新的“平面”有限耦合不动点，这表明系统的相态可能在不改变某些基本性质的情况下发生变化。这种不动点的存在对于理解量子系统的稳定性至关重要。最后，作者讨论了如何通过调整系统参数来实现这种对应关系，这为实验上操纵和控制这些复杂的量子系统提供了理论指导。这项工作加深了我们对量子线与拓扑超导体相互作用的理解，并为未来的实验和理论研究开辟了新的路径。

D. Giuliano, I. Afﬂeck / Nuclear Physics B 944 (2019) 114645 9

Disc

=2[K

]

, (11)

with the factor 2 stemming from the fourfold degeneracy due to the two MM’s in the two-

boundary version of the model and to the KF’s associated to the two QW’s. (Note that, differently

from what was done in Ref. [18], here we do not count the additional degeneracy associated with

the MM’

s at the outer boundaries of the superconducting lead, as they contribute to the g-function

just an overall factor of 2, which drops from the physically meaningful ratios between g com-

puted at two different ﬁxed points). At the disconnected ﬁxed point, the boundary Hamiltonian

describing the coupling of the QW’s to the MM is presented in bosonic coordinates as

(1)

b,B,2

=−2it



cos





(φ

(0) +φ

(0))



−2it



cos





(φ

(0) −φ

(0))



(12)

The scaling dimension of H

(1)

b,B,2

, d

, can be readily derived using the transformation in

Eqs. (A.6). The result is d

. For 1/2 <K<1 and for U>0, we ﬁnd

< 1,

which implies that H

(1)

b,B,2

always corresponds to a relevant boundary interaction. In addition,

other boundary interactions, though not present in the original (“bare”) Hamiltonian, can be

generated from the RG. The ﬁrst one corresponds to boundary normal intra-wire backscat-

tering, described by operators of the form ψ

†

R,a

(0)ψ

L,a

(0) + h.c., which are not effective,

due to Dirichlet boundary conditions on θ

(x) at x = 0. Then, one has inter-wire normal

backscattering, corresponding to operators of the form V

Normal,(1,2)

= ψ

†

R,1

(0)ψ

L,2

(0) + h.c. ∝



cos[

√

2πφ

(0)], with corresponding scaling dimension d

Normal,(1,2)

= K

−1

. Finally, one

has inter-channel pairing, corresponding to operators of the form V

Pair,(1,2)

=ψ

R,1

(0)ψ

L,2

(0) +

h.c. ∝ 



cos[

√

2πφ

(0)], with scaling dimension d

Pair,(1,2)

= K

−1

. Thus, as long as 1/2 <

, K

< 1, no relevant operators are allowed at the disconnected ﬁxed point but the boundary

coupling to the MM, H

(1)

b,B,2

The relevance of the operators in H

(1)

b,B,2

implies that, as soon as (at least one of) the t

’s are

= 0, the corresponding operator(s) trigger an RG ﬂow away from the disconnected ﬁxed point.

In Ref. [18]it is shown that, for K

< 1, the junction either ﬂow towards a ﬁxed point with type

A(N) boundary conditions in channel-1(2) (the A ⊗N ﬁxed point), or towards the complemen-

tary, N ⊗A ﬁxed point. In both cases, a straightforward implementation of our method yields,

for the g function

A⊗N

N⊗A

√

)

⇒ρ

1,1

A⊗N

Disc

√



1 −



πu





. (13)

The result in Eq. (13) corresponds to the symmetric limit of the junction discussed in Ref. [18].

Note that it also ﬁxes an error in that reference, though without affecting the ﬁnal result. The

important point is the over-all factor

√

2, which ensures that ρ

1,1

< 1as long as 1/2 <K. It

actually comes from the correct counting of the degrees of freedom associated with zero-mode

real fermion operators. In particular, for the RG ﬂow towards the A ⊗N (N ⊗ A) ﬁxed point to

occur, the bare couplings must be such that t

). In this case, the RG makes the run-

ning coupling corresponding to the larger bare coupling constant ﬂow all the way to ∞. Let us

assume this is t

. Accordingly, to recover the A ⊗N ﬁxed point, one considers the two-boundary

version of H

(1)

b,B,2

, in which t

→∞. In fact, this implies “locking” two of the four real fermions

10 D. Giuliano, I. Afﬂeck / Nuclear Physics B 944 (2019) 114645

(2 KF’s plus 2 MM’s) into a linear combination annihilating the physical states, leaving the other

two decoupled from the boundary interaction, with a total degeneracy factor of 2 in the total

partition function and, therefore, a factor

√

2in g

A⊗N

[18]. The set of allowed boundary oper-

ators at the A ⊗N ﬁxed point includes the same operators we listed at the disconnected ﬁxed

point, though realized differently, and with different scaling dimensions, due to the change in the

boundary conditions for the bosonic ﬁelds [18]. In particular, normal intra-channel 1 backscatter

ing corresponds to an operator V

Intra,1

∝cos[2

√

πθ

(0)], with scaling dimension d

Intra,1

−1

At the same time, inter-channel normal backscattering and inter-channel pairing are described by

boundary operators that are linear combinations of V

a,(1,2)

and of V

b,(1,2)

, respectively given by

a,(1,2)

=



√

π[θ

(0)−φ

(0)]

b,(1,2)

=



√

π[θ

(0)+φ

(0)]

, (14)

together with their Hermitean conjugates. The operators in Eqs. (14)have the same scaling di-

mension, d

a,(1,2)

= d

b,(1,2)

, which is consistent with the result in Eq. (D.26) of Ref. [18]. As

a result, one obtains d

a,(1,2)

= d

b,(1,2)

1+K

. For N = 2, one obtains K

= K/



1 +

πu

which is always < 1for 1/2 <K<1 and U>0. Thus, one obtains that

1+K

> 1, as long

as K

< 1. Therefore, we conclude that both inter-channel normal backscattering and inter-

channel pairing are described by irrelevant operators. Finally, an additional boundary operator

arises from the residual boundary coupling of channel 2 to the MM. This corresponds to the term

∝ t

in Eq. (12). Despite the fact that it appears to correspond to a relevant operator, due to the

hybridization between γ

and 

in the state that sets in at the A ⊗N ﬁxed point, it becomes

effective only to order t

, corresponding to an operator V

2,Res

∝ cos[2

√

πφ

(0)], with scaling

dimension d

2,Res

> 1. This eventually proves that, for K

< 1, the stable phase of the

N =2 junction either corresponds to the A ⊗N , or to the N ⊗A ﬁxed point.

An additional possibility is provided by the A ⊗ A ﬁxed point of Ref. [18], with type A

boundary conditions in both channels. The g-function at the A ⊗ A ﬁxed point can be readily

derived either from the analysis of Ref. [18](up to an over-all

√

2, as discussed above), or from

the general result of section 5, taken for N =2 and for N

=2, N

=0. As a result, one obtains

A⊗A

]

⇒



A⊗A

Disc



ˆρ

A⊗A

A⊗N



. (15)

From Eqs. (15) one readily checks that, as long as K

< 1, one obtains ρ

A⊗A

> 1, as well as

ˆρ

A⊗A

> 1, which implies that the A ⊗A ﬁxed point is unstable to both the N ⊗N , as well as to

the A ⊗N ﬁxed point. This is consistent with the DEBC results about the set of allowed boundary

operators at the A ⊗ A ﬁxed point. Indeed, implementing type A boundary conditions at x = 0

for both φ

(x) and φ

(x), we see that the boundary operators describing inter-channel normal

backscattering, as well as inter-channel pairing, are in general expressed as linear combinations

of the operators V

a,(1,2)

, V

b,(1,2)

, respectively given by

a,(1,2)

=



√

2πθ

(0)

b,(1,2)

=



√

2πθ

(0)

, (16)

together with their Hermitean conjugates. Their scaling dimensions are accordingly given by

a,(1,2)

= K

, d

b,(1,2)

= K

. Thus, we see that, for K

< 1, they both correspond to rele-

vant boundary interactions. Other boundary interaction terms are determined by the operators

D. Giuliano, I. Afﬂeck / Nuclear Physics B 944 (2019) 114645 11

Res,1

Res,2

describing the residual coupling to the MM which, as discussed in detail in Ap-

pendix B, in this case can be effective to ﬁrst-order in the boundary interaction strengths, different

from what happens at the A ⊗N ﬁxed point. In particular, on applying the bosonization proce-

dure to the operators derived in Appendix B, one obtains

Res,1

∝e



[θ

(0)+θ

(0)]

Res,2

∝e



[θ

(0)−θ

(0)]

. (17)

The corresponding scaling dimensions are readily derived to be equal to each other and given

by d

Res,1

= d

Res,2

. Given the deﬁnition of K

and K

in section 2, we see that they

are both relevant, as long as K

< 1. Incidentally, we note that the other allowed boundary

operators, corresponding to intra-channel boundary backscattering processes, are realized as

Intra,1(2)

∝ cos[2

√

πθ

1(2)

(0)] = cos[

√

2π(θ

(0) ± θ

(0))]. Accordingly, they have the same

scaling dimension, d

Intra,1

= d

Intra,2

= K

+ K

and, therefore, they are both irrelevant, for

1/2 <K and U>0.

The conclusion that, for K

< 1, there are two equivalent stable ﬁxed points in the phase

diagram of the N = 2 junction (the A ⊗ N and the N ⊗ A ﬁxed points discussed above) im-

plies that there must be a phase transition between the two of them. In Ref. [18], the phase

transition has been identiﬁed at a FCFP in the phase diagram of the junction, which is attracti

along the line in parameter space corresponding, in the symmetric case, to t

= t

, and other-

wise repulsive. To show this, an effective means is to resort to the perturbative RG approach

within the -expansion method. Basically, one assumes that the junction parameters are such that

=1 −, with 0 <1, and accordingly derives the RG equations to the ﬁrst nonlinear order

in the boundary couplings, so as to recover nontrivial zeroes for the β-functions corresponding

to the FCFP. For the details of the systematic derivation of the corresponding RG equations we

refer to Ref.

[18]in the speciﬁc case N =2, as well as to Appendix D.1 for the generalization of

the procedure to a generic N , while here we just quote the ﬁnal result. Speciﬁcally, as extensively

discussed in Appendix D.1, one introduces the dimensionless running couplings



, with

the cutoff τ

∝D

−1

, D

being a high-energy (band) cut-off for the system. Therefore, letting the

scale run from D

down to the scale parameter D<D

, one obtains that the corresponding RG

trajectories of the running couplings are determined by the differential equations

=

−F



−



=

−F



−



, (18)

with l = ln(D

/D), D being the running energy scale, and the function F (ν) deﬁned in

Eq. (D.7). In general, for small initial values of the

’s, Eq. (18) implies a growth of the

along the RG trajectories. Along the symmetric line t

= t

in parameter space, this takes the

system to the FCFP discussed in Ref. [18], which corresponds to the nontrivial zeroes of the

right-hand sides of Eqs. (18)at

= t

∗



/F



−



. Alternatively, if the initial

condition lies off the symmetric line, the RG trajectories ﬂow towards either the A ⊗N , or the

N ⊗ A, ﬁxed point, according to whether, at D = D

, one has t

, or t

. While an exact

description of the FCFP is still missing, within the -expansion method it is possible to estimate

the corresponding value of the g function to leading order in the , obtaining [18]

剩余52页未读，继续阅读

weixin_38673798

粉丝: 5
资源: 944

量子线与拓扑超导体结的相图：费米子模式与非平凡不动点

渐近安全量子引力中的手性费米子

张量Gross-Neveu模型的三维相图和不动点

全息QCD相图与纠缠熵之间的相互作用

系统相图matlab代码-geneus:通过Usadel扩散方程模拟一般非平衡超导体/铁磁体系统

1 +1维p波超导体的全息纠缠熵

全息QCD相图与相互和n部分信息之间的相互作用

移动重夸张的熵，有效弦张力和QCD相图

论文研究 - ν= 2/3双层分数阶量子霍尔系统的相图和相变的数值和解析研究

超统计和有效QCD相图

平面矩阵量子力学，张量和Sachdev-Ye-Kitaev模型的相图

最新资源