动态规划求最短路：Floyd算法与实例解析

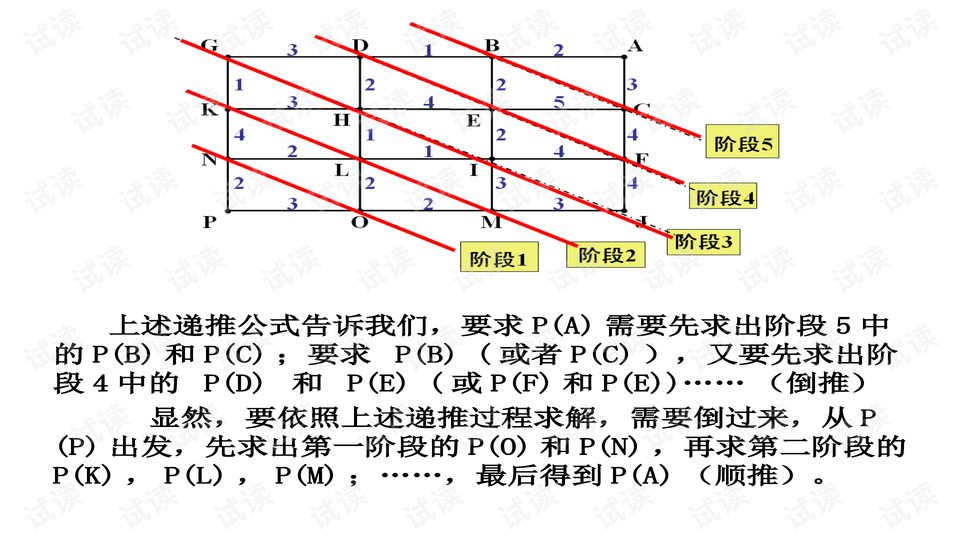
"这篇讲稿主要讲解了如何使用动态规划求解原图中任意两点间的最短路径问题，尤其在交通图中增加线路后的情况。动态规划是一种解决多阶段决策优化问题的方法，通过逐步构建最优解，确保在任何阶段的选择都是局部最优的，从而保证全局最优。讲稿中提到了Floyd算法作为初始最短路径计算，并通过三层循环迭代更新最短路径值，确保考虑所有可能的中间节点。此外，讲稿还涵盖了动态规划的基本概念、基础题型和综合题型，通过实例解析了动态规划的运用。" 在动态规划中，解决最短路径问题通常涉及到一系列阶段，每个阶段代表问题的一个状态。在这个例子中，问题的状态是交通图中两个城市之间的最短路径，而阶段则是中间节点的数量。动态规划的思路是自底向上，从基础状态开始（即没有新增线路的最短路径），逐渐增加中间节点，直到求得所有可能的最短路径。 Floyd算法是求解所有顶点对之间最短路径的经典算法，它通过迭代的方式检查每一对顶点是否存在更短的路径。在本题中，val[a, b, m]表示在增加m条线路后城市a到城市b的最短路径长度。初始时，val[a, b, 0]是原图中a到b的最短路径，可以通过Floyd算法计算得出。 在动态规划的三层循环中，外层循环k逐步增加，意味着考虑更多的中间节点；中间层循环a遍历所有城市，寻找起点；内层循环b遍历所有城市，寻找终点。如果当前节点a可以通过节点k到达节点b，并且这样的路径比之前记录的最短路径更短，那么就更新val[a, b, 0]的值。 这种解决问题的方法满足动态规划的两个关键性质：“无后效性”（一旦某个阶段的决策做出，后续阶段的决策不会影响该阶段的决策）和“最优子结构”（问题的最优解可以由子问题的最优解组合得出）。因此，动态规划是解决此类问题的合适工具。 动态规划的基础题型通常包括背包问题、最长公共子序列、矩阵链乘法等，而综合题型可能涉及到更复杂的状态转移和决策树。理解动态规划的核心在于识别问题的状态、找出状态转移方程以及确定最优子结构，这样才能有效地构造解决方案。