贝叶斯决策理论在分类器中的应用

"该资源是一份关于基于贝叶斯决策理论的分类器的演示文稿，涵盖了贝叶斯决策的基本概念、最小错误率和最小风险的决策策略、Bayes分类器与判别函数的原理，以及正态分布下的贝叶斯决策应用。" 在模式识别领域，贝叶斯决策理论是一种利用概率统计方法对样本进行分类的技术。在描述中，首先提到了模式识别的基础，即根据对象的特征值将它们归类。特征向量x由d个特征组成，形成一个d维特征空间，每个点代表一个模式样本。由于样本的不确定性和可分性的差异，有时候需要借助贝叶斯决策理论来进行更精确的分类。 贝叶斯决策理论的应用主要基于两个原因：一是样本的不确定性，包括样本本身的随机性、特征选择的不完善以及测量中的噪声；二是分类时需要考虑各类模式之间的可分性，当类别间界限模糊时，需通过统计方法评估样本属于某一类别的概率。 在贝叶斯决策理论中，有三个关键的概率概念： 1. 先验概率（Prior Probability）：在没有考虑任何证据时，事件发生的概率，可以通过训练集样本估算。 2. 类条件概率密度函数（Class-conditional Probability Density Function）：给定类别i的情况下，样本x出现的概率密度分布，也称为似然函数。 3. 后验概率（Posterior Probability）：在观察到样本x后，样本属于类别i的概率。 Bayes公式是连接这些概率的关键，它允许我们根据先验概率和类条件概率密度函数来计算后验概率，公式为： \[ P(\mathcal{C}_i|x) = \frac{P(x|\mathcal{C}_i) \cdot P(\mathcal{C}_i)}{P(x)} \] 其中，$P(\mathcal{C}_i|x)$是后验概率，$P(x|\mathcal{C}_i)$是类条件概率，$P(\mathcal{C}_i)$是先验概率，$P(x)$是样本x的边缘概率，可以被类别概率加权平均来近似。 基于Bayes决策理论的分类规则通常是选择具有最高后验概率的类别作为样本的归属类别。如果类别总体的概率分布已知，并且类别数c是确定的，那么我们可以有效地应用这种决策规则。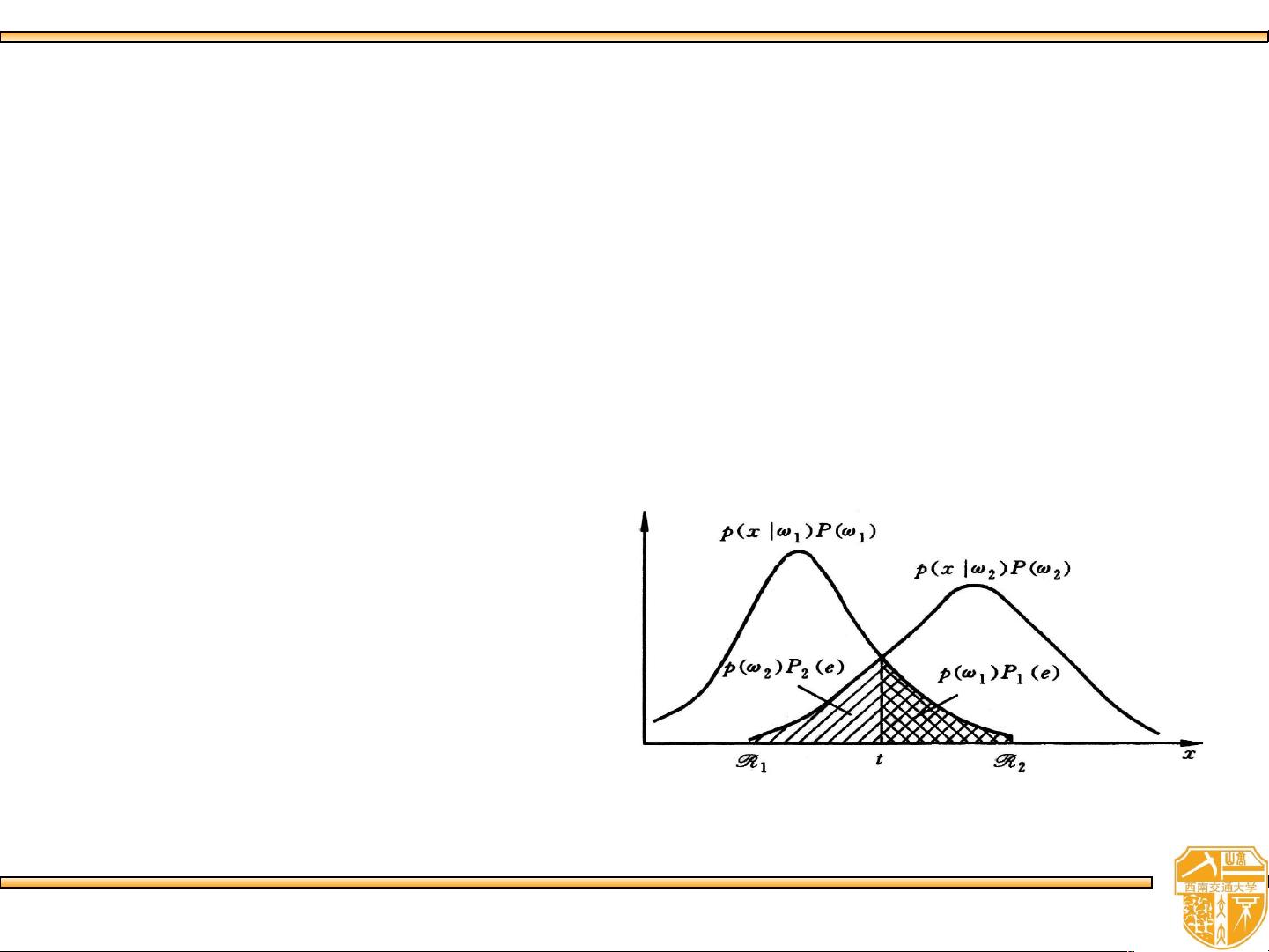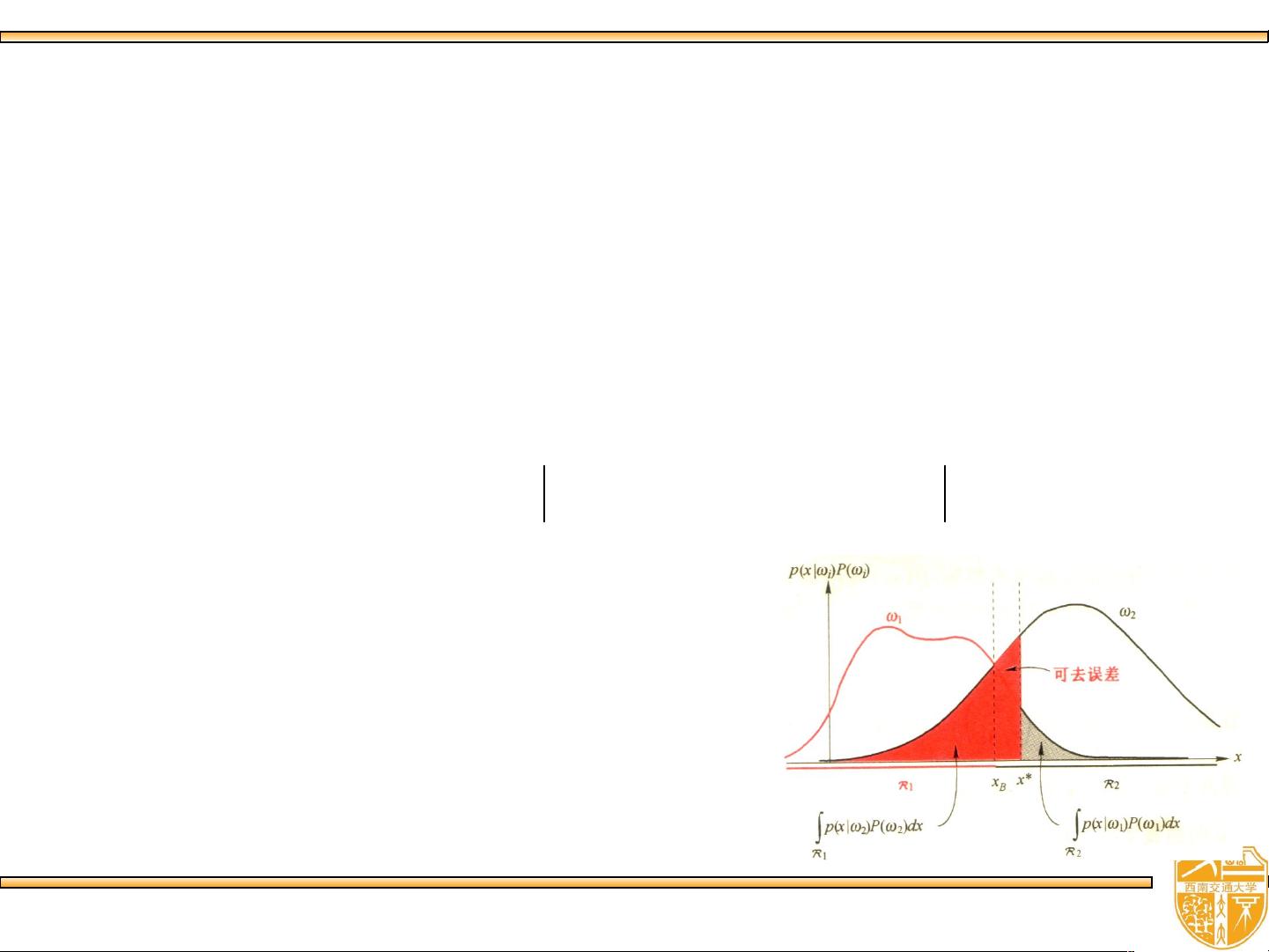 在第2章中，介绍了两种类型的贝叶斯决策： 1. 最小错误率的贝叶斯决策：选择最有可能的类别，即使这可能导致某些错误分类，但整体错误率最低。 2. 最小风险的贝叶斯决策：除了考虑错误率外，还考虑了误分类的成本，选择导致总风险最小的决策。 在第4章中，讨论了正态分布的贝叶斯决策，这是在实际应用中常见的假设，因为正态分布具有良好的数学特性，便于分析和计算。在这种情况下，可以利用正态分布的性质来更准确地估计类条件概率和后验概率，从而优化分类性能。 这份资源深入探讨了贝叶斯决策理论在分类问题中的应用，是理解贝叶斯分类器工作原理和构建实际系统的重要参考资料。