数学建模与Logistic模型在Matlab中的应用

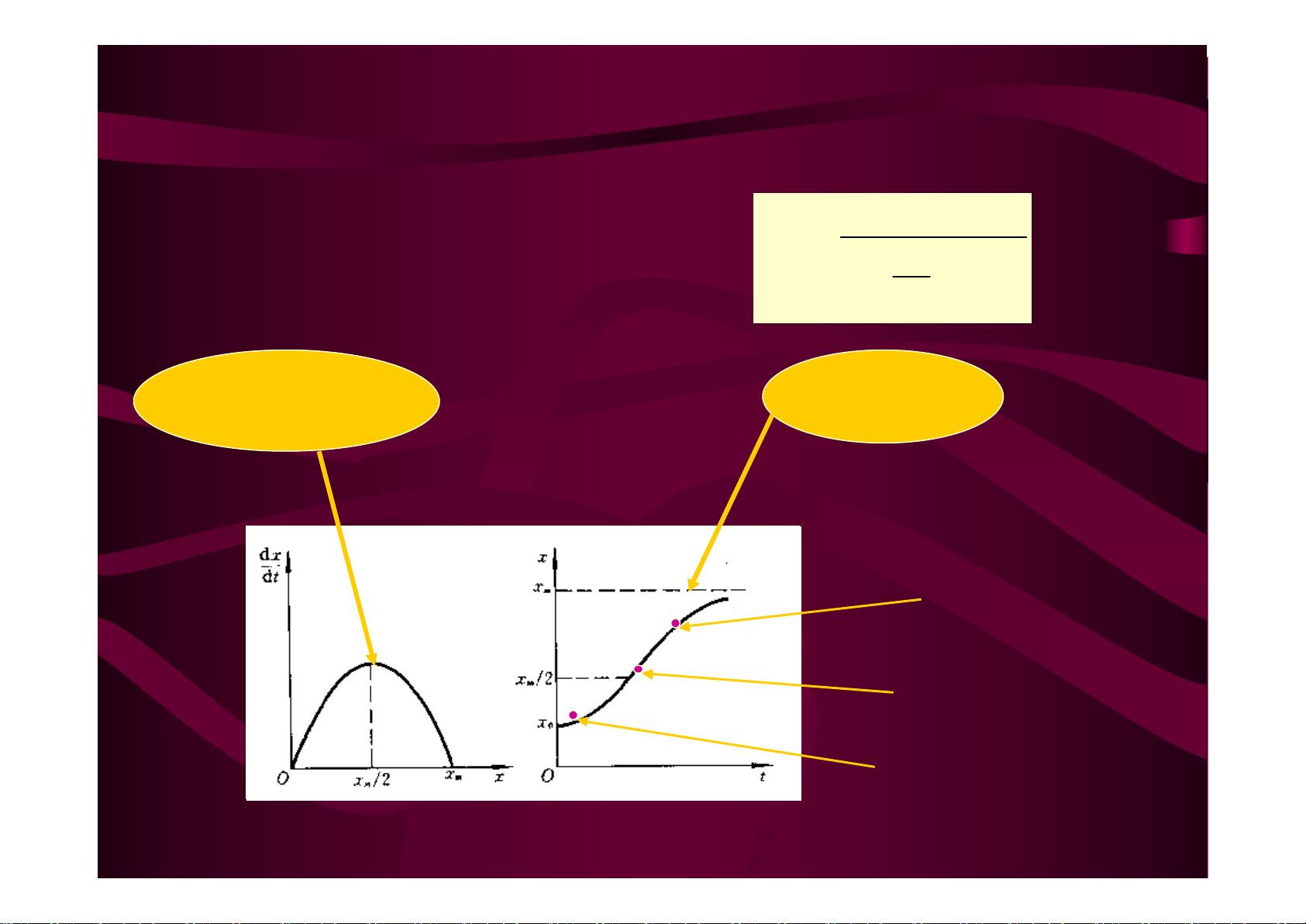
"此资源是一个关于数学建模和MATLAB应用的教程，主要涉及Logistic模型在人口预报中的应用。教程中介绍了数学建模的过程、Logistic模型的基本概念、参数估计方法以及模型的误差分析。此外，还提供了使用MATLAB进行参数估计的实践练习和实例，如水稻叶伸长生长变化的模拟。" 在数学建模中，我们将现实问题转化为数学形式，通过求解模型来解决实际问题。这个过程通常包括问题定义、模型构建、求解和模型验证。在描述中提到的一个例子是估计人体血液总量，这需要运用数学知识来推导和计算。 Logistic模型是人口预报中的一个重要工具，它包含了指数增长模型和阻滞增长模型。指数增长模型假设无限制的增长，而Logistic模型则考虑了环境的限制，引入了固有增长率和环境容纳量这两个关键概念。固有增长率代表在理想条件下种群的自然增长速度，而环境容纳量则是种群可以长期稳定生存的最大数量。 Logistic模型的微分方程表示为 \( \frac{dx}{dt} = r_x \cdot x \left(1 - \frac{x}{K}\right) \)，其中 \( r_x \) 是固有增长率，\( K \) 是环境容纳量，\( x \) 是当前种群数量。模型的解可以通过分离变量法得到，呈现出S形增长曲线，分为初始缓慢增长、指数快速增长和稳定生长三个阶段。 在实际应用中，如人口预报，需要对Logistic模型的参数进行估计。这通常采用最小二乘法，通过对历史数据的拟合来找到最佳参数值。MATLAB作为一个强大的数值计算和建模工具，可以方便地进行这种参数估计和误差分析。 教程中的课后作业要求使用P11表2的数据，分别确定指数增长模型和Logistic模型的参数，并进行误差分析。此外，还提供了使用MATLAB实现最小二乘法的练习，例如分析水稻叶伸长生长的变化，模拟出与实际观测记录相匹配的生长曲线。 这个资源不仅涵盖了数学建模的基础理论，还强调了实践操作，适合初学者和有一定基础的学习者提升技能，同时为实际问题的解决提供了一种有效的数学工具。通过学习和应用这些模型，可以加深对复杂系统动态的理解，并能应用于生物学、经济学等多个领域。