最优匹配算法与目标跟踪：匈牙利算法解析

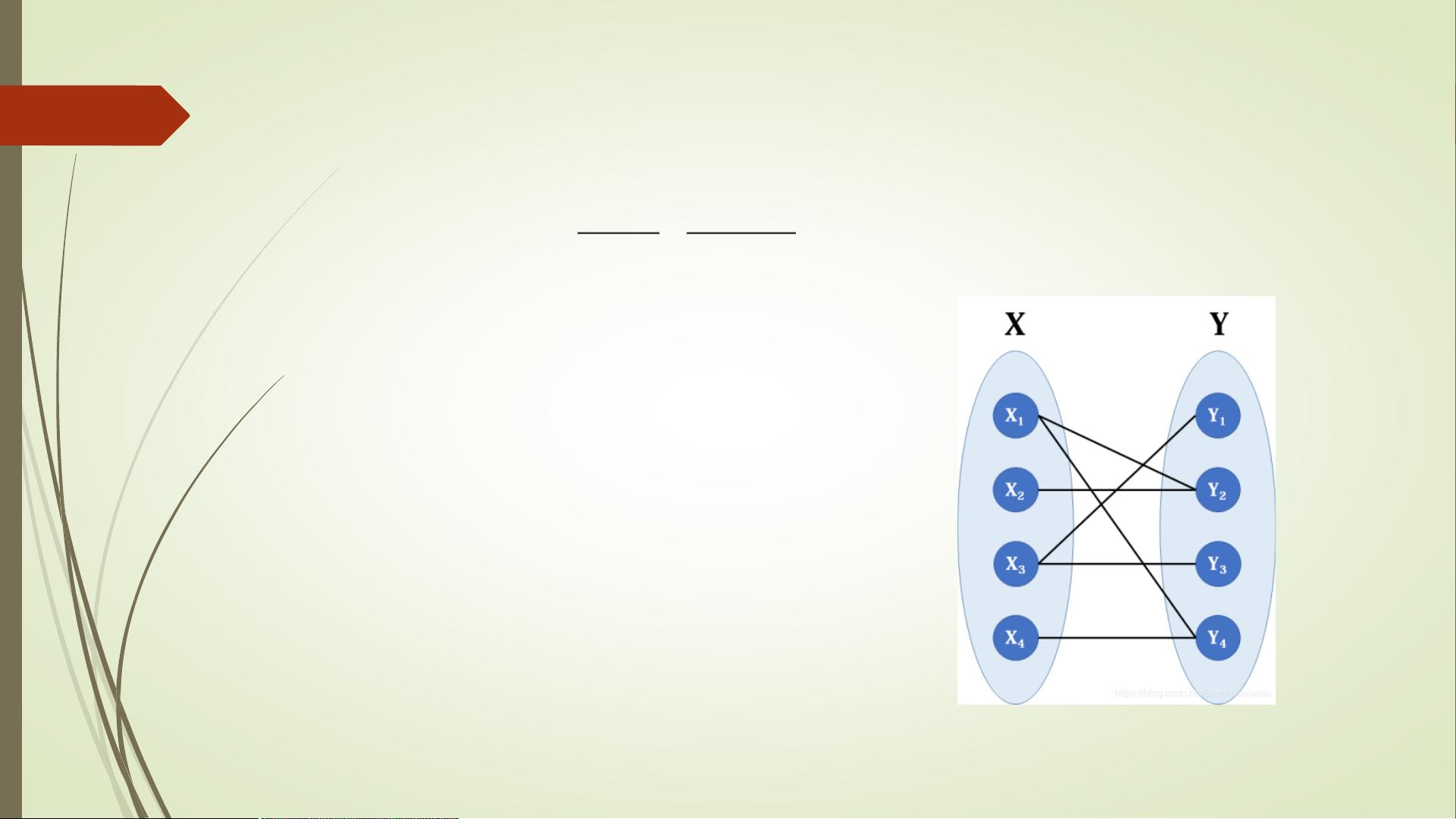
方法"。 匈牙利方法是一种经典的目标跟踪算法，主要用于解决匹配问题。在目标跟踪中，通常需要将当前帧中的目标与之前帧中的目标进行匹配，从而确定目标的运动轨迹。而匈牙利方法则提供了一种有效的解决方案，可以在时间复杂度为O(n^3)的情况下实现最优匹配。 匈牙利方法的核心思想是通过建立一个匹配矩阵来表示目标之间的相似程度。匹配矩阵的每个元素表示当前帧中的一个目标与之前帧中的一个目标的相似程度。然后，通过不断调整匹配矩阵中的元素，找到一种最佳匹配方案，使得目标之间的总相似度最大化。 具体实现匈牙利方法需要以下步骤： 1. 构建匹配矩阵：将当前帧中的目标与之前帧中的目标进行两两比较，计算它们之间的相似度，并将结果存储在匹配矩阵中。 2. 进行匹配：根据匹配矩阵，通过一定的规则进行匹配。匈牙利方法采用了一个贪心算法，即每次选择匹配矩阵中相似度最高的目标进行匹配。并在每次匹配后更新匹配矩阵，排除已经匹配的目标。 3. 重复匹配：重复执行步骤2，直到所有的目标都匹配完毕。这样就可以得到最佳匹配方案，确定目标的运动轨迹。 匈牙利方法的主要优点是在保证最优解的情况下，能够在较短的时间内完成匹配。对于目标跟踪来说，时间是非常关键的，因为需要实时更新目标的位置信息。此外，匈牙利方法还可以处理目标数量不一致的情况，即当前帧中的目标数量可以与之前帧中的目标数量不同。 然而，匈牙利方法也存在一些缺点。首先，其时间复杂度较高，随着目标数量的增加，计算量也会随之增加。其次，匹配矩阵的构建需要考虑目标之间的相似度，这对于目标跟踪而言是一个比较复杂的问题。另外，匈牙利方法对目标的运动速度比较敏感，在目标快速移动或者运动模式发生变化时，可能导致匹配结果不准确。 综上所述，匈牙利方法是一种经典有效的目标跟踪算法，尤其适用于目标数量不一致、时间关键的应用场景。然而，在实际应用中，还需要根据具体情况选择合适的方法，并结合其他算法来实现更准确、高效的目标跟踪。