椭圆最值问题解决策略探析

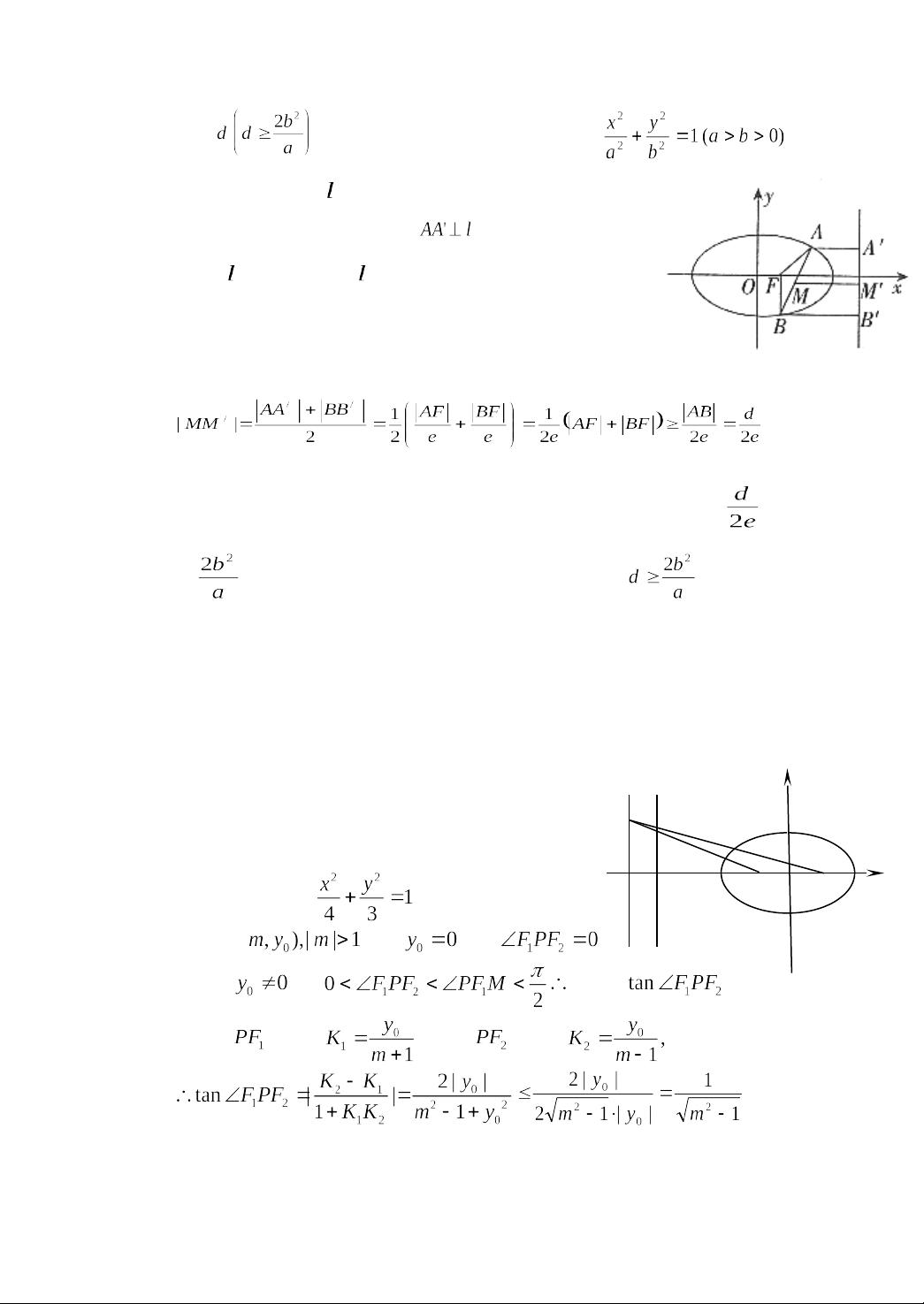
"本文详细探讨了如何破解椭圆中最值问题，包括两类常见问题：求离心率的最值和求点点（点线）的最值。文章通过具体实例和策略，介绍了解决这类问题的数学思想方法，如函数与方程思想、数形结合、转化与化归等。" 椭圆中最值问题在高中数学考试中频繁出现，是解答题的重点，也是教学难点。解决这类问题通常需要结合数学的多种思想，如将问题转化为求函数值域、解不等式或利用函数单调性。此外，平面几何中最值问题的知识也是必不可少的工具。 第一类问题涉及到求椭圆离心率的最值。离心率是椭圆的重要属性，表示椭圆的形状。解题策略包括建立点之间的关系，如在例1中，通过坐标变换和椭圆的几何性质，将角度转化为边长，再利用椭圆方程求解离心率的最值。另一种策略是利用三角函数的有界性，如例2所示，通过正弦定理和合分比定理，将几何关系转化为三角函数表达，进而求出离心率的最小值。 第二类问题是求点点或点线之间的最值，这通常涉及到距离问题。解题时可能需要构建相关的函数，然后寻找函数的最大值或最小值，或者利用平面几何中的性质，如垂线段最短、相似三角形的比例关系等。 在处理椭圆中最值问题时，建立恰当的数学模型至关重要。这可能需要将几何问题转化为代数问题，反之亦然，通过构造方程或不等式来寻找解。同时，灵活运用数形结合，将几何直观与代数精确相结合，可以大大简化问题。此外，转化与化归的思想也是解决复杂问题的关键，即将难以处理的问题转化为已知或更简单的形式。 解决椭圆中最值问题需要综合运用多种数学工具和策略，不断探索和实践，才能在面对这些挑战时找到正确的路径。通过深入理解和熟练掌握这些策略，不仅可以应对高考中的难题，还能提升对数学的理解和应用能力。